练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
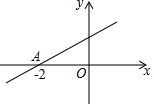
    8．如图，直线y=kx+b与x轴的交点为A（-2，0），则不等式kx+b＞0的解集为（　　）
    A．x＞2B．x≤2C．x＞-2D．x≤-2

    分析 观察函数图象得到当x＞-2时，函数图象在x轴上方，所以y＞0，即kx+b＞0．

    解答 解：当x＞-2时，y＞0，即kx+b＞0，
    所以关于x的不等式kx+b＞0的解集为x＞-2．
    故选C．

    点评 本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．2017年5月12日是第106个国际护士节，从数串“2017512”中随机抽取一个数字，抽到数字2的概率是$\frac{2}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．化简：$\frac{{x}^{2}-4}{{x}^{2}-2x+1}$•$\frac{x-1}{x-2}$-$\frac{x}{x-1}$=$\frac{2}{x-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

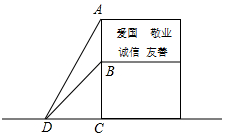    16．为了弘扬“社会主义核心价值观”，区政府在广场上竖立了如图所示的公益广告牌，并在两侧加固钢缆，已知钢缆底端D到达广告牌立柱AC的距离为5米，从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°，求广告牌的高度AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某区八年级有3000名学生参加“爱我中华”知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了部分学生的得分进行统计：
    成绩x（分）频数频率
    50≤x＜6010a
    60≤x＜70160.08
    70≤x＜80b0.20
    请你根据以上的信息，回答下列问题：
    （1）a=0.05，b=40．
    （2）在扇形统计图中，“成绩x满足50≤x＜60“对应扇形的圆心角度数是18°；
    （3）若将得分转化为等级，规定：50≤x＜60评为D，60≤x＜70评为C，70≤x＜90评为B，90≤x＜100评为A．这次全区八年级参加竞赛的学生约有1530人参赛成绩被评为“B”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：（$\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$）÷$\frac{a}{a-1}$，其中a=2sin60°-tan45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．在平面直角坐标系中，O为原点，点A（-3，0），点B（0，3），点E、点F分别为OA，OB的中点，若正方形OEDF绕点O顺时针旋转，得到正方形OE′D′F′，若直线AE′与直线BF′相交于点P，则点P的纵坐标的最大值是（　　）
    A．$\frac{\sqrt{3}+1}{2}$B．$\frac{\sqrt{3}+3}{2}$C．$\frac{\sqrt{3}+3}{4}$D．$\frac{3\sqrt{3}+3}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，直线a∥b，若∠1=55°，∠2=60°，则∠3=115°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．近几年，全社会对空气污染问题越来越重视，空气净化器的销量也在逐年增加．某商场从厂家购进了A、B两种型号的空气净化器，两种净化器的销售相关信息见下表：
    A型销售数量（台）B型销售数量（台）总利润（元）
    5102000
    1052500
    （1）每台A型空气净化器和B型空气净化器的销售利润分别是多少？
    （2）该公司计划一次购进两种型号的空气净化器共100台，其中B型空气净化器的进货量不少于A型空气净化器的2倍，为使该公司销售完这100台空气净化器后的总利润最大，请你设计相应的进货方案；
    （3）已知A型空气净化器的净化能力为300m3/小时，B型空气净化器的净化能力为200m3/小时，某长方体室内活动场地的总面积为200m2，室内墙高3m，该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新，若不考虑空气对流等因素，至少要购买A型空气净化器多少台？

    查看答案和解析>>

    同步练习册答案