
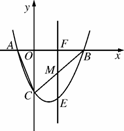
如图N212,在平面直角坐标系中,直线y=-3x-3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
解:(1)当y=0时,-3x-3=0,x=-1,∴A(-1, 0).
当x=0时,y=-3,∴C(0,-3).
∵抛物线过A,C两点,
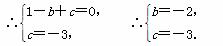
抛物线的解析式是y=x2-2x-3.
当y=0时, x2-2x-3=0,解得 x1=-1,x2=3.
∴ B(3, 0).
(2)由(1)知 B(3, 0) , C(0,-3),
直线BC的解析式是y=x-3.
设M(x,x-3)(0≤x≤3),则E(x,x2-2x-3)
∴ME=(x-3)-( x2-2x-3)=-x2+3x=- 2+
2+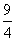 .
.
∴当x=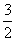 时,ME的最大值为
时,ME的最大值为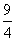 .
.
(3)不存在.由(2)知 ME 取最大值时,
ME=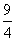 ,
,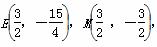
∴MF=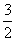 ,BF=OB-OF=
,BF=OB-OF=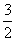 .
.
设在抛物线x轴下方存在点P,使以P,M,F,B为顶点的四边形是平行四边形,
则BP∥MF,BF∥PM.
∴P1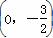 或 P2
或 P2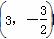 .
.
当P1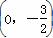 时,由(1)知y=x2-2x-3=-3≠-
时,由(1)知y=x2-2x-3=-3≠-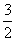 ,∴P1不在抛物线上.
,∴P1不在抛物线上.
当P2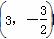 时,由(1)知y=x2-2x-3=0≠-
时,由(1)知y=x2-2x-3=0≠-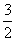 ,
,
∴P2不在抛物线上.
综上所述:在抛物线上x轴下方不存在点P,使以P,M,F,B为顶点的四边形是平行四边形


科目:初中数学 来源: 题型:
学校准备设计一款女生校服,对全校女生喜欢的颜色进行了问卷调查,统计如下表所示:
| 颜色 | 黄色 | 绿色 | 白色 | 紫色 | 红色 |
| 学生人数 | 100 | 180 | 220 | 80 | 750 |
学校决定采用红色,可用来解释这一现象的统计知识是( )
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如下的调查问卷(单选).
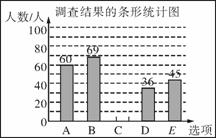
在随机调查了该市全部5000名司机中的部分司机后,统计整理并制作了如图N36的统计图.根据以下信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=________;
(2)该市支持选项B的司机大约有多少人?
(3)若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被选中的概率是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图N48中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=-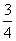 x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;
(2)若函数y=-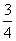 x+b(b为常数)的坐标三角形周长为16,求此三角形的面积.
x+b(b为常数)的坐标三角形周长为16,求此三角形的面积.
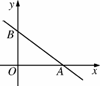
图N48
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠C=90°,∠B=30°,用直尺和圆规作出∠A的平分线与BC边交于点D(不写作法,保留作图痕迹)。在新图形中,你发现了什么?请写出两条。
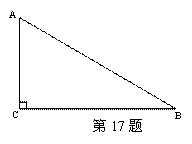 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com