
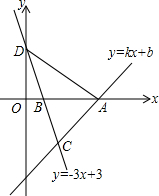
 如图,一次函数y=kx+b的图象经过点A(4,0),直线y=-3x+3与x轴交于点B,与y轴交于点D,且两直线交于点C(2,m).
如图,一次函数y=kx+b的图象经过点A(4,0),直线y=-3x+3与x轴交于点B,与y轴交于点D,且两直线交于点C(2,m).分析 (1)先把点C(2,m)代入y=-3x+3得求得m=-3,然后利用待定系数法确定一次函数的解析式;
(2)先确定直线y=-3x+3与x轴的交点坐标,然后利用S△ACD=S△ABD+S△ABC进行计算;
(3)当AP:PD=1:2时,过P作PE⊥x轴于E,当AP:PD=2:1时,过P′作P′E′⊥x轴于E′,根据相似三角形的性质即可得到结论.
解答 解:(1)把C(2,m)代入y=-3x+3得m=-3×2+3=-3;
把A(4,0),C(2,-3)代入y=kx+b得$\left\{\begin{array}{l}{4k+b=0}\\{2k+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-6}\end{array}\right.$.
所以一次函数的解析式为y=$\frac{3}{2}$x-6;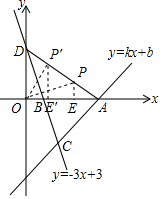
(2)对于y=-3x+3,令y=0,则x=1,则B(1,0);令x=0,则y=3,则D(0,3).
则AB=4-1=3,
则S△ACD=S△ABD+S△ABC=$\frac{1}{2}$×3×3+$\frac{1}{2}$×3×3=9;
(3)存在,
当AP:PD=1:2时,过P作PE⊥x轴于E,
∴△APE∽△ADO,
∴PE:OD=AE:OA=$\frac{1}{3}$,
∴PE=1,AE=$\frac{4}{3}$,
∴OE=$\frac{8}{3}$,
∴P($\frac{8}{3}$,1);
当AP:PD=2:1时,过P′作P′E′⊥x轴于E′,
∴△AP′E′∽△ADO,
∴P′E′=2,AE′=$\frac{8}{3}$,
∴OE′=$\frac{4}{3}$,
∴P($\frac{4}{3}$,2),
综上所述:P($\frac{8}{3}$,1)或($\frac{4}{3}$,2).
点评 本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
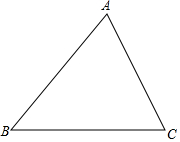 已知△ABC,利用位似变换,求作内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2(不写画法,保留画图痕迹).
已知△ABC,利用位似变换,求作内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2(不写画法,保留画图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
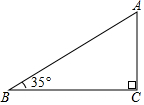 在Rt△ABC中,∠C=90°,∠B=35°,AC=20,解这个直角三角形.(边长精确到0.1,参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
在Rt△ABC中,∠C=90°,∠B=35°,AC=20,解这个直角三角形.(边长精确到0.1,参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
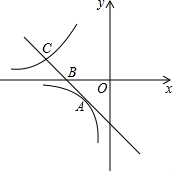 如图,直线y=-x+a与双曲线y=$\frac{4}{x}$(x<0)有唯一公共点A,与x轴于双曲线y=$\frac{k}{x}$(x<0)分别交于点B,C.
如图,直线y=-x+a与双曲线y=$\frac{4}{x}$(x<0)有唯一公共点A,与x轴于双曲线y=$\frac{k}{x}$(x<0)分别交于点B,C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com