
����Ŀ��ij������ÿ���֧������Ϊ60 Ԫ��ÿ��ij˳����� x���ˣ���ÿ���������� ��Ʊ������ ��֧�����ã�y��Ԫ���ı仯��ϵ���±���ʾ��ÿλ�˿͵ij˳�Ʊ�۹̶����䣩��
x���ˣ� | �� | 200 | 250 | 300 | 350 | 400 | �� |
y��Ԫ�� | �� | ��20 | ��10 | 0 | 10 | 20 | �� |
���ݱ����е����ݣ��ش��������⣺
��1��������仯��ϵ�У��Ա�����ʲô���������ʲô��
��2����Ҫ���������ù�����ÿ��˿��������ٴﵽ���٣�
��3�������ж�һ��˿�����Ϊ 5 00��ʱ�������Ƕ��٣�
��4�� ��д���ù�����ÿ������ y��Ԫ����ÿ��˳�����x ���ˣ��Ĺ�ϵʽ��
���𰸡���1��ÿ��ij˳�������ÿ�������3��300����3��40����4��y=![]() x-60��
x-60��
��������
��1�������Ա�����������Ķ��壬������⼴�ɽ�𣻣�2���۲�����е����ݼ��ɽ�𣻣�3���۲�����е����ݿ�֪���˳�����ÿ����50�ˣ�ÿ�����������10Ԫ���ɴ˼��ɽ�𣻣�4����ÿλ�˿͵Ĺ���Ʊ��ΪaԪ�����������y=ax-60���ڰ�x=200��y=-20����y=ax-60�����a��ֵ���ɴ˼�����øù�����ÿ������y��Ԫ����ÿ��˳�����x ���ˣ��Ĺ�ϵʽ��
��1��������仯�����У�ÿ��ij˳��������Ա�����ÿ����������������
��2�����ݱ���ɵã���ÿ��˳��������ٴﵽ300��ʱ���ù������Ų������
��3���۲�����е����ݿ�֪���˳�����ÿ����50�ˣ�ÿ�����������10Ԫ��
�൱ÿ��ij˿�����Ϊ 5 00��ʱ������Ϊ40Ԫ.
��4����ÿλ�˿͵Ĺ���Ʊ��ΪaԪ��
��������ã�y=ax-60��
��x=200��y=-20����y=ax-60��
�ã�200a-60=-20
��ã�a=![]() ��
��
��y=![]() x-60��
x-60��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��(1)��ѧ��Ϊ�˽�ijС����ͥ�¾���ˮ���,��������˸�С�����ּ�ͥ,�����������ݽ�����������,��֪��С����ˮ��������![]() �ļ�ͥռ�������ͥ�����İٷֱ�Ϊ12%�������������Ϣ����������⣺
�ļ�ͥռ�������ͥ�����İٷֱ�Ϊ12%�������������Ϣ����������⣺
���� |
|
|
|
|
|
|
�¾���ˮ�� |
|
|
|
|
|
|
Ƶ�������� | 6 | 12 |
| 10 | 4 | 2 |
��1�����ε�����õķ�ʽ�� ����ղ顱�������顱�������������� ��
��2����ȫƵ�ʷֲ�ֱ��ͼ��

��3�������������ݻ��Ƴ�����ͳ��ͼ�����¾���ˮ����![]() ����Բ�ĽǶ����� .
����Բ�ĽǶ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ��з���3�������5�������ҿڴ��з���7�������9���������������ɫ�ⶼ��ͬ����ֽ��������ڴ����ֱ�������ڴ�����������һ������Ӽ�����������ĸ�����![]() (��)����������������ĸ�����
(��)����������������ĸ�����![]() (��)��
(��)��
(1)��![]() (��)��
(��)��![]() (��)��ֵ�����Ƚ����ǵĴ�С��
(��)��ֵ�����Ƚ����ǵĴ�С��
(2)���ס��������ڴ���������ڴ�����ֽ��Ⱥ���ӱ�����������һ���Ǻ���ĸ���Ϊ![]() (��)��С����Ϊ��
(��)��С����Ϊ��![]() (��)
(��)![]()
![]() (��)
(��)![]()
![]() (��)�������뷨��ȷ����˵�����ɣ�
(��)�������뷨��ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��2x��3��x�ύ��A��B���㣨A��B����ߣ�����y�ύ�ڵ�C��
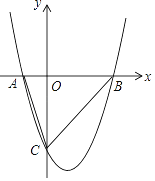
��1�������A��B��C�����꣮
��2����S��ABC
��3�����������ϣ�����C�⣩���Ƿ���ڵ�N��ʹ��S��NAB=S��ABC �� �����ڣ������N�����꣬���� ���ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DA��AB��AD��AB��EA��AC��AE��AC��
��1����˵����ACD�ա�AEB��
��2������ACB��90��������CE��
��˵��ECƽ�֡�ACB��
���ж�DC��EB��λ�ù�ϵ����˵�����ɣ�
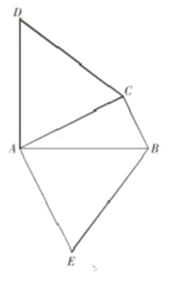
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��

��1����![]() ʱ����ͼ2����
ʱ����ͼ2����![]() �ij���
�ij���

��2����![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ���䶨����
�ĺ�����ϵʽ���䶨����
��3����![]() ����
����![]() Ϊ���ĵ��������Σ���
Ϊ���ĵ��������Σ���![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з������ʽ��Ӧ����
����![]() ,
,![]() ������Ʒ����2��
������Ʒ����2��![]() ��Ʒ��1��
��Ʒ��1��![]() ��Ʒ����80Ԫ����4��
��Ʒ����80Ԫ����4��![]() ��Ʒ��3��
��Ʒ��3��![]() ��Ʒ����180Ԫ
��Ʒ����180Ԫ
(1)��![]() ,
,![]() ������Ʒÿ�����Ƕ���Ԫ��
������Ʒÿ�����Ƕ���Ԫ��
(2)�����������![]() ,
,![]() ������Ʒ��10�����ܷ��ò�����260Ԫ����������ټ�
������Ʒ��10�����ܷ��ò�����260Ԫ����������ټ�![]() ��Ʒ��
��Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��������
��������![]() .
.


��1����![]() ��
��![]() ��������ꣻ
��������ꣻ
��2����![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() �Ḻ�����ϣ���
�Ḻ�����ϣ���![]() ��
��![]() ��ĸ������ڵ�
��ĸ������ڵ�![]() ����
����![]() �����
�����![]() �����ꣻ
�����ꣻ
��3��ƽ��ֱ��![]() ����
����![]() ����������
����������![]() ����
����![]() ����
����![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() �ϵ��������ڵĵ㣬��
�ϵ��������ڵĵ㣬��![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2��bx��c��y���ڵ�C��0��4�����Գ���x=2��x�ύ�ڵ�D������ΪM����DM=OC��OD��
��1���������ߵĽ���ʽ��
��2�����P��x,y���ǵ�һ�����ڸ��������ϵ�һ�����㣬��PCD�����ΪS����S����x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ,����xȡ����ʱ��S��ֵ�������Ƕ��٣�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com