
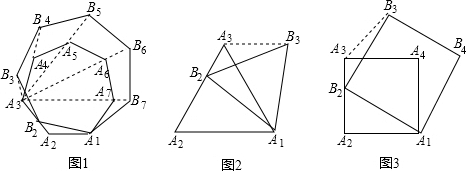
分析 (1)先判断出△A2A1B2≌△A3A1B3,再利用等边三角形的性质即可得出结论;
(2)先判断出△A3B2B3≌△DA1B2,再利用正方形的性质即可得出结论;
(3)①先判断出△A3B2B3≌△DA1B2,再利用正多边形的边相等和每个内角即可得出结论;
②利用①的结论和方法即可得出结论.
解答 (1)证明:∵△A1A2A3与△A1B2B3是正三角形,
∴A1A2=A1A3,A1B2=A1B3,∠A2A1A3=∠B2A1B3=60°,
∴∠A2A1B2=∠A3A1B3,
∴△A2A1B2≌△A3A1B3,
∴∠B3A3A1=∠A2=60°,
∴∠B3A3A1的大小不变;
(2)∠B3A3A4的大小不变,
理由:如图,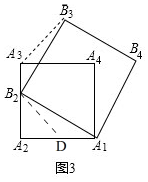 在边A1A2上取一点D,使A1D=A3B2,连接B2D,
在边A1A2上取一点D,使A1D=A3B2,连接B2D,
∵四边形A1A2A3A4与A1B2B3B4是正方形,
∴A1B2=B2B3,∠A1B2B3=∠A1A2A3=90°,
∴∠A3B2B3+∠A1B2A2=90°,∠A2A1B2+∠A1B2A2=90°,
∴∠A3B2B3=∠A2A1B2,
∴△A3B2B3≌△DA1B2,
∴∠B2A3B3=∠A1DB2,
∵A1A2=A2A3,A1D=A3B2,
∴A2B2=A2D,
∵∠A1A2A3=90°,
∴△DA2B2是等腰直角三角形,
∴∠A1DB2=135°,
∴∠B2A3B3=135°,
∵∠A4A3A2=90°,
∴∠B3A3A4=45°,
即:∠B3A3A4的大小始终不变;
(3)①∠B3A3B4的大小始终不变,理由:如图1,
在A1A2上取一点D,使A1D=A3B2,
连接B2D,
∵∠A2A1B2=180°-∠A1B2A2,∠A3B2B3=180°-∠A1B2A2,
∴∠A2A1B2=∠A3B2B3,
∵A1B2=B2B3,
∴△A3B2B3≌△DA1B2,
∴∠B2A3B3=A1DB2,
∵A1A2=A2A3,A1D=A3B2,
∴A2D=A2B2,
∴∠A1DB2=$\frac{1}{2}$(180°-∠A1A2B2)=90°-$\frac{1}{2}$×$\frac{180°(n-2)}{n}$=90°-$\frac{90°(n-2)}{n}$
∴∠B3A3A4=∠A1DB2-∠B2A3A4=90°-$\frac{90°(n-2)}{n}$-$\frac{180°(n-2)}{n}$=$\frac{180°}{n}$;
②由①知,∠B3A3A4=$\frac{180°}{2}$,
同①的方法可得,∠B4A4A5=$\frac{180°}{n}$×2,∠B5A5A6=$\frac{180°}{n}$×3,…,∠BnAnA1=$\frac{180°}{n}$×(n-2),
∴①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1
=$\frac{180°}{n}$+$\frac{180°}{n}$×2+$\frac{180°}{n}$×3+…$\frac{180°}{n}$×(n-2)=$\frac{90°(n-1)(n-2)}{n}$,
故答案为$\frac{90°(n-1)(n-2)}{n}$.
点评 此题主要考查了全等三角形的判定和性质,等边三角形的性质,正方形的性质,正多边形的性质,解本题的关键是判断出△A3B2B3≌△DA1B2,用类比的思想解决问题是解决本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:填空题
已知地球上七大洲的总面积约为150000000km2,则数字150000000用科学记数法可以表示为____________ 。
查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列各数: 3.14159, 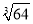 ,
, 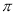 ,
, 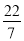 ,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
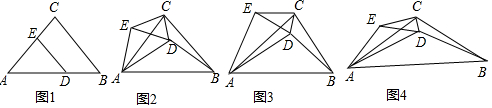
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
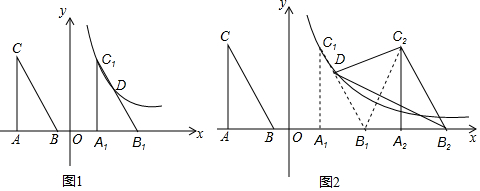
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
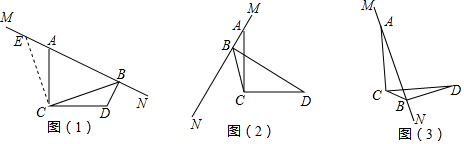
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com