
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
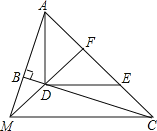
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
【答案】(1)证明见解析(2)垂直,理由见解析
【解析】
试题分析:(1)根据等腰直角三角形的性质得出DF⊥AE,DF=AF=EF,进而利用全等三角形的判定得出△DFC≌△AFM(AAS),即可得出答案;
(2)由(1)知,∠MFC=90°,FD=EF,FM=FC,即可得出∠FDE=∠FMC=45°,即可理由平行线的判定得出答案.
(1)证明:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF,
又∵∠ABC=90°,
∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
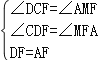 ,
,
∴△DFC≌△AFM(AAS),
∴CF=MF,
∴∠FMC=∠FCM;
(2)AD⊥MC,
理由:由(1)知,∠MFC=90°,FD=FA=FE,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥CM,
∴AD⊥MC.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数![]() (k为常数,k≠0)的图象相交点A(1,3).
(k为常数,k≠0)的图象相交点A(1,3).
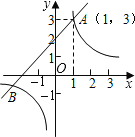
(1)求这两个函数的解析式及其图象的另一交点B的坐标;
(2)观察图象,写出使函数值y1≥y2的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,以AB为直径作⊙O,BD∥OC交⊙O于D点,CD与AB的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
(3)在(2)的条件下,如图2,AD交BC、OC分别于F、G,求![]() 的值.
的值.
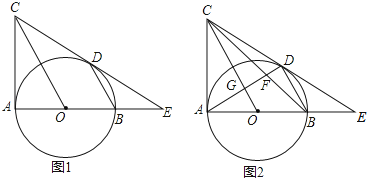
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AEBE=CEED;③CA2=CECD;④CD=BD+AD.其中正确的个数是( )
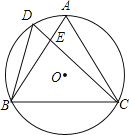
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “打开电视机,它正在播广告”是必然事件
B. “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件
C. 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行
D. 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:
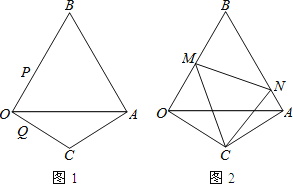
(1)在运动过程中,△OPQ的面积记为S,请用含有时间t的式子表示S.
(2)在等边△OAB的边上(点A除外),是否存在点D,使得△OCD为等腰三角形?如果存在,这样的点D共有 个.
(3)如图2,现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着点C旋转,使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于A、B两点,△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B的对应点B′坐标为( )
x+4与x轴、y轴分别交于A、B两点,△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B的对应点B′坐标为( )

A.(3,4) B.(7,4) C.(7,3) D.(3,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程.已知2013年投资1000万元,预计2015年投资1210万元.求这两年内平均每年投资增长的百分率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com