
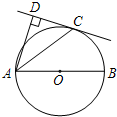
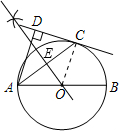
 如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.| 5 |
| 1 |
| 2 |
| 5 |
| AC2-CD2 |
| 5 |
| AE |
| AD |
| EO |
| DC |
| AE•DC |
| AD |
2
| ||
| 8 |
| 5 |
| 5 |


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
| 2 |
| ||
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
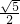 米,旗杆AB高为3米,C点的垂
米,旗杆AB高为3米,C点的垂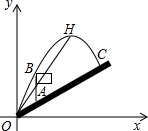 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:解答题
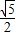 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
查看答案和解析>>
科目:初中数学 来源:2001年青海省中考数学试卷(解析版) 题型:解答题
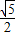 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.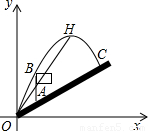
查看答案和解析>>
科目:初中数学 来源:2012年人教版初中数学九年级上25.2列举法求概率练习卷(解析版) 题型:解答题
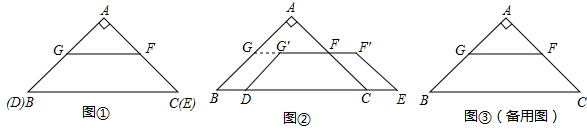
如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:

(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com