
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.

【答案】(1) B(![]() ,2).(2)证明见解析.
,2).(2)证明见解析.
【解析】
试题分析:(1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可
试题解析:(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=![]() ,
,
∴B(![]() ,2).
,2).
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=![]() NB=ND,
NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.



 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线l1:y=﹣ ![]() x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.
x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各组数据能判断是直角三角形的是( )
A. 三边长都为2B. 三边长分别为2,3,2
C. 三边长分别为13,12,5D. 三边长分别为4,5,6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 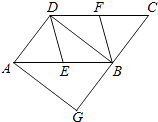
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com