
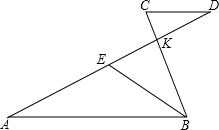
 如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点,
如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点,分析 (1)根据比例的性质得到$\frac{KC}{BK}$=$\frac{3}{7}$,根据相似三角形的性质计算即可;
(2)连接BD,取BD的中点F,连接EF交BC于G,根据三角形的中位线定理得到GF=$\frac{1}{2}$CD,EF=$\frac{1}{2}$AB,根据平行线的性质、角平分线的定义得到EG=$\frac{1}{2}$BC,即可得到答案;
(3)连接BD,作EF∥AB交BC于G,交BD于F,根据比例的性质、仿照(2)的作法解答即可.
解答 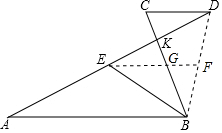 解:(1)∵BK=$\frac{7}{3}$KC,
解:(1)∵BK=$\frac{7}{3}$KC,
∴$\frac{KC}{BK}$=$\frac{3}{7}$,
∵AB∥CD,
∴△CKD∽△BKA,
∴$\frac{CD}{AB}$=$\frac{KC}{BK}$=$\frac{3}{7}$;
(2)猜想:AB=BC+CD.
证明:连接BD,取BD的中点F,连接EF交BC于G,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG=$\frac{1}{2}$BC,而GF=$\frac{1}{2}$CD,EF=$\frac{1}{2}$AB,
∵EF=EG+GF,
即:$\frac{1}{2}$AB=$\frac{1}{2}$BC+$\frac{1}{2}$CD;
∴AB=BC+CD;
(3)猜想:AB=$\frac{1}{n-1}$BC+$\frac{1}{n-1}$CD.
证明:连接BD,作EF∥AB交BC于G,交BD于F,
∵AE=$\frac{1}{n}$AD,
∴$\frac{DE}{AD}$=$\frac{n-1}{n}$,
∵EF∥AB,
∴$\frac{EF}{AB}$=$\frac{DE}{AD}$=$\frac{n-1}{n}$,即EF=$\frac{n-1}{n}$AB,
∵EF∥AB,AB∥CD,
∴EF∥CD,
同理,BG=$\frac{1}{n}$BC,GF=$\frac{1}{n}$CD,
∵EF=EG+GF,
即:$\frac{n-1}{n}$AB=$\frac{1}{n}$BC+$\frac{1}{n}$CD;
∴AB=$\frac{1}{n-1}$BC+$\frac{1}{n-1}$CD.
点评 本题考查了平行线的性质,三角形中位线定理,相似三角形的判定与性质,角平分线的性质.关键是构造平行线,找出由特殊到一般探索规律.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
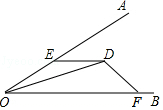 如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,
如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
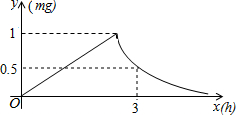 为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.
为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com