
【题目】如图,AB=AC,AB的垂直平分线交AB于D,交AC于E,BE恰好平分△ABC,有以下结论:(1)ED=EC;(2)△BEC的周长等与2AE+EC;(3)图中共有3个等腰三角形;(4)∠A=36°,其中正确的共有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】(1)由题意可知DE⊥AB,BE平分∠ABC,
∴当EC⊥BC时,有ED=EC,
∵AB=AC,
∴∠ACB不可能等于90°,
∴ED=EC不正确;
(2)∵E在线段AB的垂直平分线上,
∴EA=EB,
∴∠A=∠ABE,
∵∠ABE=![]() ∠ABC,∠BEC=∠A+∠ABE,
∠ABC,∠BEC=∠A+∠ABE,
∴∠BEC=∠ABC,
∵AB=AC,∴∠ABC=∠C,
∴∠C=∠BEC,∴BE=BC,
∴EC+EB+BC=EC+EA+EA =2EA+EC ,
∴(2)正确;
(3)∵AB=AC,
∴△ABC为等腰三角形,∠C=∠ABC,
∵EA=EB,
∴△EAB为等腰三角形,∠A=∠ABE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠C=2∠CBE,
又∠BEC=∠A+∠ABE=2∠CBE,
∴∠BEC=∠C,
∴BE=BC,
∴△BEC为等腰三角形,
∴图中共有3个等腰三角形,
∴(3)正确;
(4)由(3)可得∠BEC=∠C=2∠EBC,
∴2∠EBC+2∠EBC+∠EBC=180°,
∴∠EBC=36°,
∴∠A=∠ABE=∠EBC=36°,
∴(4)正确;
∴正确的有(2)(3)(4)共三个,
故选B.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕.
(1)求CM的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有红、黄、蓝三种颜色的球(除颜色外其余都相同),
其中红球有1个,蓝球有1个,现从中任意摸出一个是红球的概率为![]() .
.
(1)求袋中黄球的个数.
(2)第一次摸出一个球(放回),第二次再摸一个球,请用画树状图或列表法求两次摸到都是红球的概率.
(3)若规定每次摸到红球得5分,每次摸到黄球得3分,每次摸到蓝球得1分,小芳摸6次球(每次摸1个球,摸后放回)合计得20分,请直接写出小芳有哪几种摸法?(不分球颜色的先后顺序)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四种说法中,①ab是一次单项式;②单项式﹣x2y的系数是﹣1;③1+x2﹣4x是按x的降幂排列的;④数字3是单项式.不正确的是( )
A.①③
B.②③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
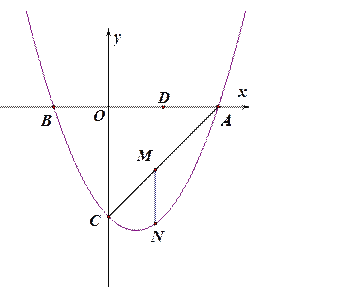
【题目】如图,抛物线![]() 与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于
与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于![]() 轴,交AC于点M.
轴,交AC于点M.
(1) 求直线AC的解析式;
(2)当点N运动至抛物线的顶点时,求此时MN的长;
(3)设点N的横坐标为t,MN的长度为l;
①求l与t之间的函数关系式,并写出t的取值范围;
②l是否存在最值,有如有写出最值;
(4)点D是点B关于![]() 轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
若存在,请求出此时△CAN的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com