
分析 (1)原式利用平方根、立方根定义计算即可得到结果;
(2)原式化简后,合并即可得到结果;
(3)原式利用绝对值的代数意义,零指数幂运算法则,平方根、立方根定义计算即可得到结果;
(4)原式利用二次根式的乘法法则计算即可得到结果.
解答 解:(1)原式=4+3-10=-3;
(2)原式=$\sqrt{2}$+2$\sqrt{2}$-6$\sqrt{2}$=-3$\sqrt{2}$;
(3)原式=3+1-3+2=3;
(4)原式=$\sqrt{48}$+$\sqrt{18}$-2$\sqrt{2}$=4$\sqrt{3}$+3$\sqrt{2}$-2$\sqrt{2}$=4$\sqrt{3}$+$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
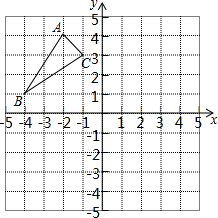 如图的方格纸中,△ABC的顶点坐标分别为A(-2,5),B(-4,1)和C (-1,3).
如图的方格纸中,△ABC的顶点坐标分别为A(-2,5),B(-4,1)和C (-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
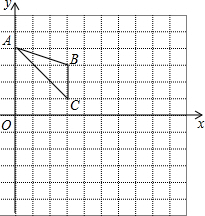 已知△ABC在平面直角坐标系中的位置,如图所示,A和点C的坐标分别为A(0,4)、C(3,1).
已知△ABC在平面直角坐标系中的位置,如图所示,A和点C的坐标分别为A(0,4)、C(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com