
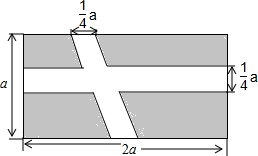
 小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草
小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草分析 (1)草地的面积就是长为(2a-$\frac{1}{4}$a)宽为(a-$\frac{1}{4}$a)的长方形的面积;
(2)路面的面积是长为2a,宽为$\frac{1}{4}$a的长方形的面积加上底为$\frac{1}{4}$a,高为a的平行四边形的面积,再减去底和高为$\frac{1}{4}$a的平行四边形的面积,计算结果与上面的结果比较得出答案即可.
解答 解:(1)(2a-$\frac{1}{4}$a)(a-$\frac{1}{4}$a)
=$\frac{7}{4}$a•$\frac{3}{4}$a
=$\frac{21}{16}$a2;
(2)路面面积:2a•$\frac{1}{4}$a+a•$\frac{1}{4}$a-$\frac{1}{4}$a•$\frac{1}{4}$a
=$\frac{11}{16}$a2;
∵$\frac{11}{16}$a2×2>$\frac{21}{16}$a2;
∴这块草坪的设计没达到要求.
点评 此题考查整式的混合运算,利用长方形和平行四边形的面积计算方法是解决问题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题



查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在梯形ABCD中,已知AD∥BC,梯形各边长为:AB=6,BC=9,CD=4,DA=3,分别以AB、CD为直径作圆,则这两圆的位置关系是( )
如图,在梯形ABCD中,已知AD∥BC,梯形各边长为:AB=6,BC=9,CD=4,DA=3,分别以AB、CD为直径作圆,则这两圆的位置关系是( )| A. | 内切 | B. | 相交 | C. | 外离 | D. | 外切 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com