
分析 (1)当x2-2=0时,分式$\frac{x}{{x}^{2}-2}$没有意义;
(2)当x2-12≠0时,分式$\frac{1}{{x}^{2}-12}$有意义.
解答 解:(1)当x2-2=0时,
解得x=$\sqrt{2}$或-$\sqrt{2}$,
∴当x=$\sqrt{2}$或-$\sqrt{2}$时,分式$\frac{x}{{x}^{2}-2}$没有意义;
(2)当x2-12≠0时,
解得x≠2$\sqrt{3}$或-2$\sqrt{3}$,
∴当x≠2$\sqrt{3}$或-2$\sqrt{3}$时,分式$\frac{1}{{x}^{2}-12}$有意义.
故答案为:$\sqrt{2}$或-$\sqrt{2}$;≠2$\sqrt{3}$或-2$\sqrt{3}$.
点评 此题主要考查了分式有意义的条件,要熟练掌握,解答此题的关键是要明确:分式有意义的条件是分母不等于零.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
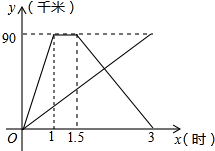 如图中,甲、乙两人同时从相距90千米的A地前往B地.甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后原路返回A地,如图是他们离A地的距离y(千米)与x(时间)之间的函数关系图象.
如图中,甲、乙两人同时从相距90千米的A地前往B地.甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后原路返回A地,如图是他们离A地的距离y(千米)与x(时间)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,分别以AC,BC所在直线为轴,把Rt△ABC旋转1周得到两个圆锥.设这两个圆锥的全面积分别为S1,S2,比较S1与S2的大小,并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,分别以AC,BC所在直线为轴,把Rt△ABC旋转1周得到两个圆锥.设这两个圆锥的全面积分别为S1,S2,比较S1与S2的大小,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com