
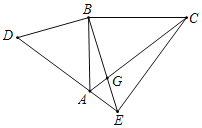
【题目】如图,已知Rt△ABC中,两条直角边AB=3,BC=4,将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE,并且点A落在DE边上,则△BEC的面积=__________________
【答案】![]() .
.
【解析】
过B作BP⊥AD于P,BQ⊥AC于Q,依据∠BAD=∠BAC,即AB平分∠DAC,可得BP=BQ,进而得出BP=![]() ,AD=
,AD=![]() ,S△ABD=
,S△ABD=![]() AD×BP=
AD×BP=![]() ,再根据△ABD∽△CBE,可得
,再根据△ABD∽△CBE,可得![]() ,即可得到S△CBE=
,即可得到S△CBE=![]() .
.
如图,过B作BP⊥AD于P,BQ⊥AC于Q,
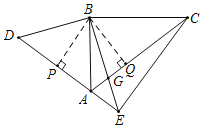
由旋转可得,∠CAB=∠D,BD=BA=3,
∴∠D=∠BAD,
∴∠BAD=∠BAC,即AB平分∠DAC,
∴BP=BQ,
又∵Rt△ABC中,AB=3,BC=4,
∴AC=5,BQ=![]() ,
,
∴BP=![]() ,
,
∴Rt△ABP中,AP=![]() ,
,
∴AD=![]() ,
,
∴S△ABD=![]() AD×BP=
AD×BP=![]() ,
,
由旋转可得,∠ABD=∠CBE,DB=AB,EB=CB,
∴△ABD∽△CBE,
∴![]() ,即
,即![]() ,
,
解得S△CBE=![]() ,
,
故答案为:![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】将![]() 的边
的边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,边
,边![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() ,连接
,连接![]() ,作
,作![]() 的中线
的中线![]() .
.
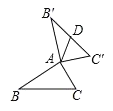
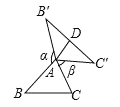

图① 图② 图③
(初步感知)
(1)如图①,当![]() ,
,![]() 时,
时,![]() 的长为 ;
的长为 ;
(探究运用)
(2)如图②,![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
(应用延伸)
(3)如图③,已知等腰![]() ,
,![]() ,延长
,延长![]() 到
到![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一周得到
顺时针旋转一周得到![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的长度(用含
的长度(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解题)在解分式方程![]() 时,小明的解法如下:
时,小明的解法如下:
解:方程两边都乘以x﹣3,得2﹣x=﹣1﹣2①.移项得﹣x=﹣1﹣2﹣2②.解得x③.
(1)你认为小明在哪一步出现了错误? (只写序号),错误的原因是 .
(2)小明的解题步骤完善吗?如果不完善,说明他还缺少哪一步?答: .
(3)请你解这个方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
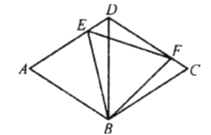
【题目】如图,菱形![]() 的边长为2,对角线
的边长为2,对角线![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的两个动点,且满足
上的两个动点,且满足![]() .
.
(1)求证: ![]() ;
;
(2)判断![]() 的形状,并说明理由,同时指出
的形状,并说明理由,同时指出![]() 是由
是由![]() 经过如何变换得到.
经过如何变换得到.
查看答案和解析>>
科目:初中数学 来源: 题型:
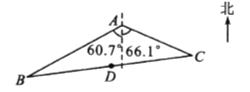
【题目】如图,湿地景区岸边有三个观景台![]() 、
、![]() 、
、![]() .已知
.已知![]() m,
m, ![]() m,点
m,点![]() 位于点
位于点![]() 的南偏西60. 7°方向,点
的南偏西60. 7°方向,点![]() 位于点
位于点![]() 的南偏东66. 1°方向.
的南偏东66. 1°方向.
(1)求![]() 的面积;
的面积;
(2)景区规划在线段![]() 的中点
的中点![]() 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道![]() .试求
.试求![]() 、
、![]() 间的距离.(结果精确到0. 1 m,参考数据:
间的距离.(结果精确到0. 1 m,参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)计算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)计算:![]()
(3)化简:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化简:3x2﹣[7x﹣(4x﹣3)﹣2x2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com