
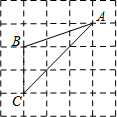
 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
如图,△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{2\sqrt{5}}{5}$ |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
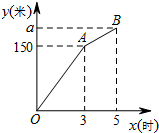 甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.
甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+a3=a5 | B. | 4a+2b=6ab | C. | ${(\frac{1}{{{a^2}+1}})^0}=1$ | D. | ${(2\sqrt{5})^2}=10$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com