
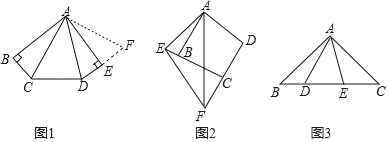
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
【答案】(1)△AFD,CD=DE+BC;(2EF=DF﹣BE,理由见解析;(3)![]() .
.
【解析】
(1)如图1,将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌△AFD,可得结论;
(2)如图2,将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',证明△AFE≌△AFE',据全等三角形的性质解答;
(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',根据全等三角形的性质、勾股定理计算.
(1)BC,CD,DE之间的数量关系为:DF=DE+BC,理由是:
如图1,将△ABC绕点A逆时针旋转90°至△AEF,
由∠B=∠AED=∠AEF=90°,得∠DEF=180°,即点D,E,F三点共线,
∵∠BAE=90°,∠CAD=45°,
∴∠BAC+∠DAE=∠DAE+∠EAF=45°,
∴∠CAD=∠FAD,
∵AD=AD,
∴△ACD≌△FAD(SAS),
∴CD=DF=DE+EF=DE+BC,
故答案为:△AFD,CD=DE+BC;
(2)如图2,EF,BE,DF之间的数量关系是EF=DF﹣BE.

证明:将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',
则△ABE≌△ADE',
∴∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,
∴∠EAE'=∠BAD,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∠ADE'=∠ADC,即E',D,F三点共线,
又∠EAF=![]() ∠BAD=
∠BAD=![]() ∠EAE'
∠EAE'
∴∠EAF=∠E'AF,
在△AEF和△AE'F中,
 ,
,
∴△AFE≌△AFE'(SAS),
∴FE=FE',
又∵FE'=DF﹣DE',
∴EF=DF﹣BE;
(3)如图3,
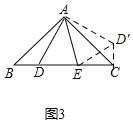
将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',则CD'=BD=2,
由(1)同理得,△AED≌AED',.
∴DE=D'E.
∵∠ACB=∠B=∠ACD'=45°,
∴∠ECD'=90°,
在Rt△ECD'中,ED'=![]() ,即DE=
,即DE=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
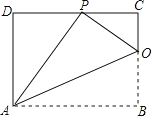
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:![]() ;
;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购买A、B两种奖品,奖励成绩优异的同学.已知购买1件A奖品和1件B奖品共需18元;购买30件A奖品和20件B奖品共需480元.
(1)A、B两种奖品的单价分别是多少元?
(2)如果学校购买两种奖品共100件,总费用不超过850元,那么最多可以购买A奖品多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.
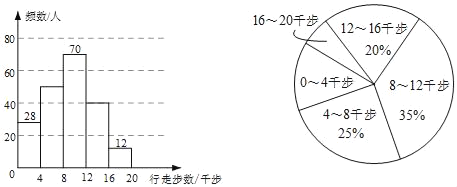
根据统计图,得出下面四个结论:
①此次一共调查了200位小区居民;
②行走步数为8~12千步的人数超过调查总人数的一半;
③行走步数为4~8千步的人数为50人;
④扇形图中,表示行走步数为12~16千步的扇形圆心角是72°.
其中正确的结论有( )
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=12,C是线段AB上一点,分别以AC、CB为边在A的同侧作等边△ACP和等边△CBQ,连接PQ,则PQ的最小值是( )
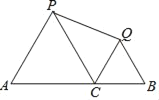
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
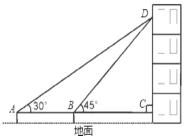
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A.B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度
(计算结果精确到0.1米,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F.则EF的最小值为_____
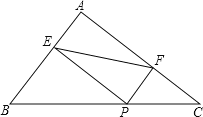
查看答案和解析>>
科目:初中数学 来源: 题型:
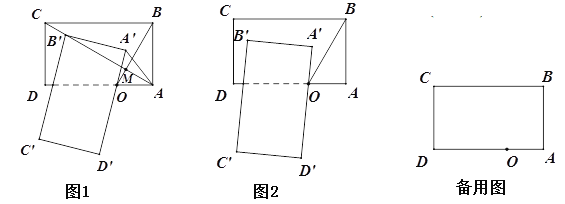
【题目】如图:已知矩形ABCD中,AB=![]() cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转
cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转![]() 角(
角(![]() ),得到矩形A′B′C′D′
),得到矩形A′B′C′D′
(1)求证:AC⊥OB;
(2)如图1, 当B′落在AC上时,求AA′;
(3)如图2,求旋转过程中△CC′D′的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com