
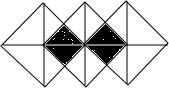
 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 一定是对角线交点 | B. | 一定在对角线上 | ||
| C. | 一定在对边中点的连线上 | D. | 可以是任意位置 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com