
分析 (1)首先通分进而合并分子,进而化简求出即可;
(2)首先将括号里面通分进而利用分式除法运算法则化简求出即可;
(3)首先化简二次根式进而合并同类二次根式求出即可;
(4)首先化简二次根式,进而利用二次根式乘除运算法则求出即可;
(5)首先化简二次根式进而合并同类二次根式求出即可;
(6)首先将分子与分母能分解因式的进行分解因式,进而化简求出即可;
(7)首先化简二次根式进而合并同类二次根式求出即可;
(8)首先将括号里面通分进而利用分式除法运算法则化简求出即可;
(9)首先化简二次根式进而合并二次根式乘法运算法则求出即可.
解答 解:(1)$\frac{b}{a-b}$+$\frac{a}{a+b}$+$\frac{2ab}{{a}^{2}-{b}^{2}}$
=$\frac{b(a+b)}{(a+b)(a-b)}$+$\frac{a(a-b)}{(a+b)(a-b)}$+$\frac{2ab}{{a}^{2}-{b}^{2}}$
=$\frac{{a}^{2}+{b}^{2}+2ab}{(a+b)(a-b)}$
=$\frac{a+b}{a-b}$;
(2)($\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$)÷$\frac{x}{x-1}$
=[$\frac{(x+1)(x-1)}{(x-1)^{2}}$+$\frac{1}{{x}^{2}-2x+1}$]×$\frac{x-1}{x}$
=$\frac{{x}^{2}}{(x-1)^{2}}$×$\frac{x-1}{x}$
=$\frac{x}{x-1}$;
(3)$\sqrt{12}$-$\sqrt{18}$-$\sqrt{0.5}$+$\sqrt{\frac{1}{3}}$
=2$\sqrt{3}$-3$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{3}$
=$\frac{7\sqrt{3}}{3}$-$\frac{7\sqrt{2}}{2}$;
(4)$\frac{1}{3}$$\sqrt{{x}^{2}y}$×(-$\frac{1}{4}$$\sqrt{\frac{{y}^{2}}{x}}$)÷(-$\frac{1}{6}$$\sqrt{{x}^{2}y}$)
=$\frac{x}{3}\sqrt{y}$×(-$\frac{y}{4x}$$\sqrt{x}$)×(-6$\sqrt{\frac{1}{{x}^{2}y}}$)
=($\frac{x}{3}$×$\frac{y}{4x}$×6)$\sqrt{xy×\frac{1}{{x}^{2}y}}$
=$\frac{y}{2}$$\sqrt{\frac{1}{x}}$
=$\frac{y}{2x}$$\sqrt{x}$;
(5)$\sqrt{18}$-$\sqrt{\frac{9}{2}}$-$\frac{\sqrt{3}+\sqrt{6}}{\sqrt{3}}$+$\sqrt{(1-\sqrt{2})^{2}}$
=3$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$-1-$\sqrt{2}$+$\sqrt{2}$-1
=$\frac{3\sqrt{2}}{2}$-2;
(6)$\frac{{x}^{2}+x}{x}$$÷(x+1)+\frac{{x}^{2}-x-2}{x-2}$
=$\frac{x(x+1)}{x}$×$\frac{1}{x+1}$+$\frac{(x-2)(x+1)}{x-2}$
=1+x+1
=x+2;
(7)$\sqrt{125}$+$\sqrt{\frac{5}{9}}$-$\sqrt{\frac{1}{2}}$-4$\sqrt{2}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$
=5$\sqrt{5}$+$\frac{\sqrt{5}}{3}$-$\frac{\sqrt{2}}{2}$-4$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$
=$\frac{16\sqrt{5}}{3}$-$\frac{11\sqrt{2}}{2}$+$\sqrt{3}$;
(8 )$\frac{x+3}{2x-4}$÷($\frac{5}{x-2}$-x-2)
=$\frac{x+3}{2(x-2)}$÷[$\frac{5}{x-2}$-$\frac{(x+2)(x-2)}{x-2}$]
=$\frac{x+3}{2(x-2)}$×$\frac{x-2}{(3-x)(3+x)}$
=-$\frac{1}{6+2x}$;
(9)$\frac{3}{2}$$\sqrt{20}$•(-15)•(-$\frac{1}{3}$$\sqrt{48}$)
=3$\sqrt{5}$×(-15)×(-$\frac{1}{3}$×4$\sqrt{3}$)
=60$\sqrt{15}$.
点评 此题主要考查了分式的混合运算以及二次根式的混合运算,正确因式分解以及化简二次根式是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
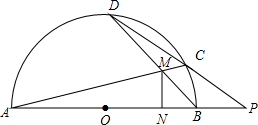 如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.
如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34≤T≤37 | B. | 34≤T≤35 | C. | 33≤T≤35 | D. | 35≤T≤37 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水价格 | 污水处理费 | |
| 每户每月用水量 | 单价:元∕吨 | 单价:元∕吨 |
| 20吨及以下 | a | 0.60 |
| 超过20吨但不超过30吨的部分 | b | 0.60 |
| 超过30吨的部分 | 3.60 | 0.60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{5}$ | D. | $\sqrt{40}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com