
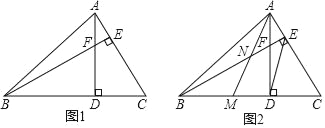
����Ŀ����ͼ1���������ABC�У���ABC=45�㣬����AD��BE�ཻ�ڵ�F��
��1���ж�BF��AC��������ϵ��˵�����ɣ�
��2����ͼ2������ACD���߶�AD���ۣ���C����BD�ϵĵ�M��AM��BE�ཻ�ڵ�N����DE��AMʱ���ж�NE��AC��������ϵ��˵�����ɣ�
���𰸡���1��BF=AC�����ɼ���������2��NE=![]() AC�����ɼ�����.
AC�����ɼ�����.
�������������������1����ͼ1��֤����ADC�ա�BDF��AAS�����ɵ�BF=AC��
��2����ͼ2�����۵��ã�MD=DC���ȸ�����������λ�ߵ����ۿɵã�AE=EC�����߶δ�ֱƽ���ߵ����ʵã�AB=BC�����ABE=��CBE����ϣ�1���ã���BDF�ա�ADM�����DBF=��MAD�����֤����ANE=��NAE=45�㣬��AE=EN������EN=![]() AC��
AC��
���������
��1��BF=AC�������ǣ�
��ͼ1����AD��BC��BE��AC��
���ADB=��AEF=90����
�ߡ�ABC=45����
���ABD�ǵ���ֱ�������Σ�
��AD=BD��
�ߡ�AFE=��BFD��
���DAC=��EBC��
����ADC����BDF��
��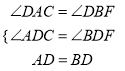 ��
��
���ADC�ա�BDF��AAS����
��BF=AC��
��2��NE=![]() AC�������ǣ�
AC�������ǣ�
��ͼ2�����۵��ã�MD=DC��
��DE��AM��
��AE=EC��
��BE��AC��
��AB=BC��
���ABE=��CBE��
�ɣ�1���ã���ADC�ա�BDF��
�ߡ�ADC�ա�ADM��
���BDF�ա�ADM��
���DBF=��MAD��
�ߡ�DBA=��BAD=45����
���DBA����DBF=��BAD����MAD��
����ABE=��BAN��
�ߡ�ANE=��ABE+��BAN=2��ABE��
��NAE=2��NAD=2��CBE��
���ANE=��NAE=45����
��AE=EN��
��EN=![]() AC��
AC��
�����͡������
��������
17
����Ŀ����֪x1��x2�Ƿ���2x2��2nx+![]() n��n+4��=0���������ң�x1��1����x2��1����1=
n��n+4��=0���������ң�x1��1����x2��1����1=![]() ����n��ֵ��
����n��ֵ��
 �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��12������18��+����7����
��2��3![]() +����2
+����2![]() ��+5
��+5![]() +����8
+����8![]() ����
����
��3������![]() ��������
��������![]() ��+����
��+����![]() ������
������![]() ����
����
��4������![]() ��������1
��������1![]() ��������2
��������2![]() ����
����
��5��42������![]() ��+����
��+����![]() ��������0.25����
��������0.25����
��6������1��10��3+����2��3��4��145��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��1���Խ���AC��BD�ཻ�ڵ�O������O��EF��AC�ֱ�����AD������CB�ڵ�E�͵�F������CE��AF��
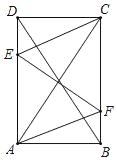
��1����֤���ı���AFCE�����Σ�
��2������E��F�ֱ��ڱ�AD��BC��ʱ�������AD��x������AFCE�������y����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��3�������ODE�ǵ��������Σ���AD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
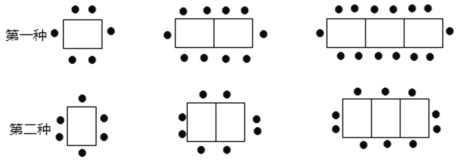
����Ŀ��ij�����У�һ�����ӿ���6�ˣ����������ְڷŷ�ʽ��
��1������n������ʱ�����ְڷŷ�ʽ�����������ˣ�
��2��һ���������Ҫ�Ӵ�70λ�˿�ͬ�Ͳͣ�������ֻ��18�������IJ�������������������ľ����������ѡ�����ַ�ʽ���ڷŲ�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���������ABC�У���ABC=45�㣬����AD��BE�ཻ�ڵ�F��
��1���ж�BF��AC��������ϵ��˵�����ɣ�
��2����ͼ2������ACD���߶�AD���ۣ���C����BD�ϵĵ�M��AM��BE�ཻ�ڵ�N����DE��AMʱ���ж�NE��AC��������ϵ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˳ij��ѧΪ�˽���꼶ѧ��������״�����Ӱ��꼶ѧ���������ȡ����ѧ���������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ������������ͳ��ͼ�е���Ϣ�ش��������⣺
��1�����γ������鹲��ȡ�˶�����ѧ����
��2������Խ��ΪC�ȼ���ѧ����������ȫ����ͼ��
��3��������ѧ���꼶����700��ѧ����������Ƹ���ѧ���꼶ѧ�������ܲ��Խ��ΪD�ȼ���ѧ���ж�������
��4����������ΪA�ȼ���2������2��Ů��������ij�ȡ2��ѧ������Ϊ��У�����˶�Ա���ص���������б�������״ͼ�ķ���������ȡ������ǡ�ö��������ĸ��ʣ�
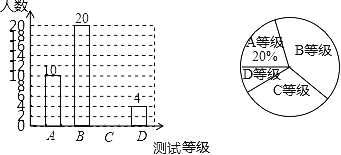
���𰸡���1��50����2��16����3��56��4��������
�����������������
��1������ͳ��ͼ�е���Ϣ��֪�����A�ȵ���10�ˣ�ռ���������20%���ɴ˼��ɼ�������ѧ����������
��2���ɣ�1���м��������ͳ��ͼ����֪��A��B��D�����ȼ��������������C�ȼ������������ɴ˲�ȫ����ͳ��ͼ��
��3���ɣ�1������õı����ѧ�������������D�ȼ�����4�˿ɼ�������D�ȼ���������ռ�İٷֱȣ��������800���п��ܻ��D�ȼ���������
��4������������ΪA1��A2������Ů��ΪB1��B2����������ͼ�����������������ʣ�
���������
��1��10��20%=50������
�𣺱��γ������鹲��ȡ��50��ѧ��.
��2��50-10-20-4=16������
�𣺲��Խ��ΪC�ȼ���ѧ����16��.
ͼ��ͳ��ͼ������������ͼ��ʾ��
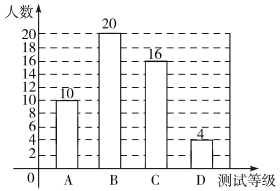
��3��700��![]() =56������
=56������
�𣺹��Ƹ���ѧ���꼶ѧ�������ܲ��Խ��ΪD�ȼ���ѧ����56��.
��4������״ͼ����������ΪA�ȼ������������ֱ�Ϊ![]() ������ΪA�ȼ�������Ů���ֱ�Ϊ
������ΪA�ȼ�������Ů���ֱ�Ϊ![]() ,
,![]() ,����״ͼ���£�
,����״ͼ���£�
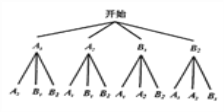
����״ͼ��֪������12 �ֽ����ÿ�ֽ�����ֵĿ�������ͬ������ȡ�����˶��������Ľ�������֣���![]() ������
������![]() ,
,![]() ��, ��P����ȡ��������������=
��, ��P����ȡ��������������=![]() .
.
�����͡������
��������
20
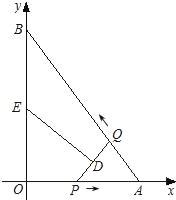
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��x�ύ�ڵ�A����y�ύ�ڵ�B����OA=3��AB=5����P�ӵ�O������OA��ÿ��1����λ�����ٶ����A�����˶��������A��������ԭ�����ٶ���AO���أ���Q�ӵ�A������AB��ÿ��1����λ�����ٶ����B�����˶���������P��Q���˶���DE���ִ�ֱƽ��PQ���ҽ�PQ�ڵ�D��������QB��BO��OP�ڵ�E����P��Qͬʱ����������Q�����Bʱֹͣ�˶�����PҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0����
��1����ֱ��AB�Ľ���ʽ��
��2���ڵ�P��O��A�˶��Ĺ����У����APQ�����S��t֮��ĺ�����ϵʽ������д��t��ȡֵ��Χ����
��3���ڵ�E��B��O�˶��Ĺ����У�����������⣺
���ı���QBED�ܷ��Ϊֱ�����Σ����ܣ������t��ֵ�������ܣ���˵�����ɣ�
�ڵ�DE������Oʱ������ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴������㴫ͳ�Ļ���ijУ��֯800��ѧ���μ���һ�Ρ�������д�����������������в���ѧ���ijɼ���������60�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������������ѧ���ijɼ���Ϊ�������ɼ����£�
90��92��81��82��78��95��86��88��72��66��62��68��89��86��93��83��100��73��76��80��77��81��86��75��82��85��71��68��74��98��90��97��85��84��78��73��65��92��96��60
�������ɼ��������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
60��x��70 | 6 | 0.15 |
70��x��80 | a | b |
80��x��90 | 14 | 0.35 |
90��x��100 | c | d |
�����������Ϣ������������⣺
��1��a���� ����d���� ����
��2���벹ȫƵ���ֲ�ֱ��ͼ
��3�����ɼ���90�����ϣ�����90�֣���Ϊ���ŵȣ�������Ʋμ���α�����800��ѧ���гɼ����š��ȵ�Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y=2x��ͼ����һ�κ��� ![]() ��ͼ���ڵ�A��m,2��,һ�κ�����ͼ����B��-2��-1����y�ύ��ΪC��x�ύ��ΪD.
��ͼ���ڵ�A��m,2��,һ�κ�����ͼ����B��-2��-1����y�ύ��ΪC��x�ύ��ΪD.
��1����һ�κ����Ľ���ʽ��
��2����![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ(![]() ����2)���ݵ�x��
����2)���ݵ�x��![]() ʱ��y��x���������С����a+b+c��0�У�������ȷ����( )
ʱ��y��x���������С����a+b+c��0�У�������ȷ����( )

A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com