
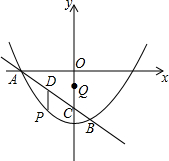
 如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.
如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.分析 (1)利用坐标轴上点的坐标特征求出A点和C点坐标,然后利用待定系数法求抛物线解析式;
(2)延长PD交x轴于E,作PF⊥AB于F,如图1,设点P(m,$\frac{1}{4}$m2-4)(-4<m<1),则D(m,-$\frac{3}{4}$m-3),接着表示出PD=-$\frac{1}{4}$m2-$\frac{3}{4}$m+1,然后证明Rt△PDF∽Rt△ACO,利用相似比得到PF=-$\frac{1}{5}$m2-$\frac{3}{5}$m+$\frac{4}{5}$,然后利用二次函数的性质解决问题;
(3)讨论:当以P、Q、C、D为顶点的四边形为菱形PCDQ时,PC=PD,利用两点间的距离公式得到m2+($\frac{1}{4}$m2-4+3)2=(-$\frac{1}{4}$m2-$\frac{3}{4}$m+1)2,解方程求出m得到P点坐标,再计算出PD的长,然后计算出OQ的长,从而得到Q点坐标;当以P、Q、C、D为顶点的四边形为菱形PQCD时,DC=DP,利用两点间的距离公式得到m2+(-$\frac{3}{4}$m-3+3)2=(-$\frac{1}{4}$m2-$\frac{3}{4}$m+1)2,解法与前面一样去确定P点和Q点的坐标.
解答 解:(1)当y=0时,-$\frac{3}{4}$x-3=0,解得x=4,则点A的坐标为(-4,0),
当x=0时,y=-$\frac{3}{4}$x-3=-3,则点C的坐标为(0,-3),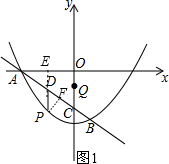
将A(-4,0)、B(1,-$\frac{15}{4}$)代入y=ax2+c得$\left\{\begin{array}{l}16a+c=0\\ a+c=-\frac{15}{4}\end{array}\right.$,解得$\left\{\begin{array}{l}a=\frac{1}{4}\\ c=-4\end{array}\right.$,
所以抛物线的解析式为y=$\frac{1}{4}$x2-4;
(2)延长PD交x轴于E,作PF⊥AB于F,如图1,
在Rt△AOC中,∵OA=4,OC=3,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
设点P(m,$\frac{1}{4}$m2-4)(-4<m<1),则D(m,-$\frac{3}{4}$m-3),
∴PD=-$\frac{3}{4}$m-3-($\frac{1}{4}$m2-4)=-$\frac{1}{4}$m2-$\frac{3}{4}$m+1,
∵∠ADE=∠PDF,∠DAE=∠PFD,
∴∠DPF=∠EAD,
∴Rt△PDF∽Rt△ACO,
∴$\frac{PF}{OA}$=$\frac{PD}{AC}$,即$\frac{PF}{4}$=$\frac{-\frac{1}{4}{m}^{2}-\frac{3}{4}m+1}{5}$,
∴PF=-$\frac{1}{5}$m2-$\frac{3}{5}$m+$\frac{4}{5}$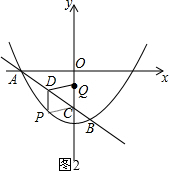
=-$\frac{1}{5}$(m+$\frac{3}{2}$)2+$\frac{5}{4}$,
当m=-$\frac{3}{2}$时,PE有最大值,最大值为$\frac{5}{4}$;
即点P到直线AB的距离的最大值是$\frac{5}{4}$;
(3)存在.
当以P、Q、C、D为顶点的四边形为菱形PCDQ时,PC=PD,如图2,
即m2+($\frac{1}{4}$m2-4+3)2=(-$\frac{1}{4}$m2-$\frac{3}{4}$m+1)2,
整理得6m2-7m-24=0,解得m1=-$\frac{3}{2}$,m2=$\frac{8}{3}$(舍去),
此时P点坐标为(-$\frac{3}{2}$,-$\frac{55}{16}$),
PD=$\frac{25}{16}$,
∴CQ=$\frac{25}{16}$,
∴OQ=3-$\frac{25}{16}$=$\frac{23}{16}$,
∴Q(0,-$\frac{23}{16}$);
当以P、Q、C、D为顶点的四边形为菱形PQCD时,DC=DP,
即m2+(-$\frac{3}{4}$m-3+3)2=(-$\frac{1}{4}$m2-$\frac{3}{4}$m+1)2,
-$\frac{1}{4}$m2-$\frac{3}{4}$m+1=±$\frac{5}{4}$m,
当-$\frac{1}{4}$m2-$\frac{3}{4}$m+1=$\frac{5}{4}$m,解得m1=-4+2$\sqrt{5}$,m2=-4-2$\sqrt{5}$(舍去),
此时P点坐标为(-4+2$\sqrt{5}$,5-4$\sqrt{5}$),对应的Q点坐标为(0,$\frac{4-5\sqrt{5}}{2}$);
当-$\frac{1}{4}$m2-$\frac{3}{4}$m+1=-$\frac{5}{4}$m,解得m1=1-$\sqrt{5}$,m2=1+$\sqrt{5}$(舍去),
此时P点坐标为(1-$\sqrt{5}$,$\frac{-5-\sqrt{5}}{2}$),对应的Q点坐标为(0,$\frac{-7-5\sqrt{5}}{4}$);
综上所述,满足条件的点为P($-\frac{3}{2}$,$-\frac{55}{16}$),Q(0,$-\frac{23}{16}$)或P($1-\sqrt{5}$,$\frac{{-5-\sqrt{5}}}{2}$),Q(0,$\frac{{-7-5\sqrt{5}}}{4}$)或P($-4+2\sqrt{5}$,$5-4\sqrt{5}$),Q(0,$\frac{{4-5\sqrt{5}}}{2}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和一次函数图象上点的坐标特征;会利用待定系数法求二次函数解析式;理解坐标与图形性质,记住两点间的距离公式;灵活运用相似比表示线段之间的关系;利用菱形的性质和分类讨论的思想解决(3)小题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
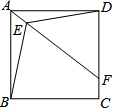 如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.
如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
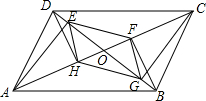 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 110°,70° | B. | 105°,75° | C. | 100°,70° | D. | 110°,80° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com