
分析 首先把分式进行通分,可得$\frac{{b}^{2}+{a}^{2}}{{a}^{2}{b}^{2}}$,再根据完全平方公式可得$\frac{(a+b)^{2}-2ab}{(ab)^{2}}$,然后再代入a+b=6,ab=2可得答案.
解答 解:$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$
=$\frac{{b}^{2}+{a}^{2}}{{a}^{2}{b}^{2}}$
=$\frac{(a+b)^{2}-2ab}{(ab)^{2}}$
=$\frac{36-4}{4}$
=8.
故答案为:8.
点评 此题主要考查了分式的化简求值,关键是掌握分式的通分和完全平方公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰好能拼成一个四边形.
如图1,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰好能拼成一个四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
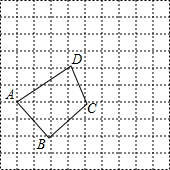 如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上.
如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$
(1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com