
����Ŀ����ͼ������ĵ�λ����Ϊ1��
![]()
��1�������B��D��ʾ������Ϊ�෴������ôͼ�е�A����D��ʾ�����ֱ��� �� ��
��2������BΪԭ��ʱ�����������Ƿ���ڵ�M��ʹ�õ�M����A�ľ����ǵ�M����D�ľ����2���������ڣ��������ʱ��M����ʾ�������������ڣ�˵�����ɣ�
��3�� �ڣ�2���������£���A����C�ֱ���2����λ����/���0.5����λ����ͬʱ�����˶���ͬʱ��P��ԭ�������3����λ����/����ٶ������˶�������A���C֮��ľ���Ϊ3����λ����ʱ�����P����Ӧ�����Ƕ��٣�
���𰸡���1����4��2 ����2��2��10 ����3����18��4��
��������
���⣨1���ɵ�B��D��ʾ������Ϊ�෴�������Ե�BΪ��2��DΪ2�����AΪ��4��
��2�����ڣ�������������۽��
��3���赱��A���C֮��ľ���Ϊ3����λ����ʱ���˶�ʱ��Ϊt��A���˶�������2+2t��C���˶�����3+0.5t����AC=3���������ۣ����ɽ��
����������⣺��1������B��D��ʾ������Ϊ�෴��������BΪ��2��DΪ2������AΪ��4���ʴ�Ϊ����4��2��
��2�����ڣ���ͼ��

����M��A��D֮��ʱ����M��ʾ����Ϊx����x������2��=2��4��x��
��ã�x=2������M��A��D�Ҳ�ʱ����x������2��=2��x��4������ã�x=10�����Ե�M����ʾ����Ϊ2��10��
��3���赱��A���C֮��ľ���Ϊ3����λ����ʱ���˶�ʱ��Ϊt��A���˶�������2+2t��C���˶�����3+0.5t������2+2t����3+0.5t��=3����ã�t=6������P���Ӧ�˶��ĵ�λ����Ϊ��3��6=18�����Ե�P��ʾ����Ϊ��18��
��3+0.5t������2+2t��=3����ã�t=![]() ������P���Ӧ�˶��ĵ�λ����Ϊ��3��
������P���Ӧ�˶��ĵ�λ����Ϊ��3��![]() =4�����Ե�P��ʾ����Ϊ��4��
=4�����Ե�P��ʾ����Ϊ��4��
�𣺵�P��ʾ����Ϊ��18��4��


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O������D���Խ���BD�Ĵ��߽�BA���ӳ����ڵ�E��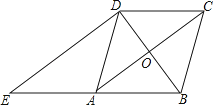
��1��֤�����ı���ACDE��ƽ���ı��Σ�
��2����AC=8��BD=6�����ADE���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���6����ȫ��ͬ��С������Գɵ�һ�������壬��ͼ��ʾ��

��1���뻭����������������ͼ��
��2�������˼���A�ı������Ϻ��ᣨ���������ϵ�һ�治�磩�������������Ǻ�ɫ��С��������____����
��3������һ��������B�뼸����A������ͼ������ͼ��ͬ����С�����������ȼ�����A��1��������______������. ����ͼ2�л���������B�ĸ���ͼ���ܵ����ֲ�ͬ���Σ�
��4�������������ͷ����һЩ��ͬ��С������������ڼ�����A�ϣ�Ҫ��������ͼ������ͼ���䣬����������___________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�DΪBC��һ�㣬��BAD=��ABC����ADC=��ACD������BAC=63����������DAC����ADC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ�����еĺɻ�������Ҫ�����˺ɻ�������A��B��������ľ���(���Dz���ֱ������)�����������ѧ֪ʶ���Ծ��ߺͲ����Ϊ�����������һ�ֲ���������
Ҫ��(1)��������ƵIJ���ƽ��ͼ��
(2)����������������д������������(������![]() ����ʾ���Ƕ���
����ʾ���Ƕ���![]() ����ʾ)��
����ʾ)��
(3)��������������ݣ�����A��B��������ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=40�㣬��ABC����ǡ�CBD��ƽ����BE��AC���ӳ����ڵ�E��
��1�����CBE�Ķ�����
��2������D��DF��BE����AC���ӳ����ڵ�F�����F�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
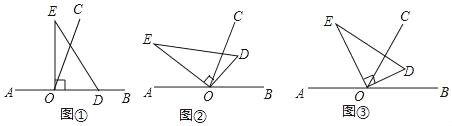
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��BOC=70������һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE=90�㣩
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=�� ���㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ�ã���OCǡ��ƽ�֡�BOE�����COD�Ķ�����
��3����ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�Oת�������ODʼ���ڡ�BOC���ڲ����Բ����BOD�͡�COE��������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1�����㣺��22+| ![]() ��4|+��
��4|+�� ![]() ����1+2tan60�㣮
����1+2tan60�㣮
��2���Ȼ�������ֵ���� ![]() ��
�� ![]() ����
���� ![]() ������x�Dz���ʽ3x+7��1�ĸ������⣮
������x�Dz���ʽ3x+7��1�ĸ������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=1����BAC=45�㣬��AEF���ɡ�ABC�Ƶ�A��˳ʱ�뷽����ת�õ��ģ�����BE��CF�ཻ�ڵ�D�� 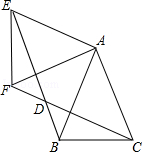
��1����֤��BE=CF��
��2�����ı���ACDEΪ����ʱ����BD�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com