
 如图,在△ABC中,AD是∠BAC的外角平分线,P是AD上异于点A的任一点,试比较PB+PC与AB+AC的大小,并说明理由.
如图,在△ABC中,AD是∠BAC的外角平分线,P是AD上异于点A的任一点,试比较PB+PC与AB+AC的大小,并说明理由. 分析 可在BA的延长线上取一点E,使AE=AC,得出△ACP≌△AEP,从而将四条不同的线段转化到一个三角形中进行求解,即可得出结论.
解答 解:PB+PC>AB+AC.
如图,在BA的延长线上取一点E,使AE=AC,连接EP,
由AD是∠BAC的外角平分线,可知∠CAP=∠EAP,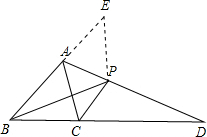
又AP是公共边,AE=AC,
在△ACP与△AEP中,
$\left\{\begin{array}{l}{AE=AC}\\{∠EAP=∠CAP}\\{AP=AP}\end{array}\right.$,
∴△ACP≌△AEP(SAS),
从而有PC=PE,在△BPE中,PB+PE>BE,
而BE=AB+AE=AB+AC,
故PB+PE>AB+AC,
所以PB+PC>AB+AC.
点评 本题主要考查了全等三角形的判定及性质以及三角形三边关系的问题,做出恰当的辅助线是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的对角线AC与BD相交于点M,矩形MNPQ与矩形ABCD全等,射线MN与MQ分别交BC边于E、F两点,若AB=2,求证:$\frac{1}{M{E}^{2}}$+$\frac{1}{M{F}^{2}}$=1.
如图,矩形ABCD的对角线AC与BD相交于点M,矩形MNPQ与矩形ABCD全等,射线MN与MQ分别交BC边于E、F两点,若AB=2,求证:$\frac{1}{M{E}^{2}}$+$\frac{1}{M{F}^{2}}$=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是利用平面直角坐标系画出的怀柔城区附近部分乡镇分布图.若这个坐标系分别以正东、正北方向为x轴、y轴的正方向.表示南华园村的点坐标为(0,-1),表示下园村的点的坐标为(1.6,0.9),则表示下列各地的点的坐标正确的是( )
如图是利用平面直角坐标系画出的怀柔城区附近部分乡镇分布图.若这个坐标系分别以正东、正北方向为x轴、y轴的正方向.表示南华园村的点坐标为(0,-1),表示下园村的点的坐标为(1.6,0.9),则表示下列各地的点的坐标正确的是( )| A. | 石厂村(-1.2,-2.7) | B. | 怀柔镇(0.4,1) | C. | 普法公园(0,0) | D. | 大屯村(2.2,2.6) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在平面直角坐标系中.
已知:如图,在平面直角坐标系中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com