
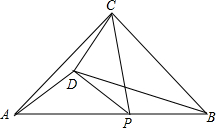
 如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.
如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.分析 (1)①点D在△ABC内部时,作PE⊥AB交BC于E,证出△PBE是等腰直角三角形,∠ACD+∠1=45°,得出∠ACD=∠2,因此∠ACD+∠APC=90°;
②当点D在△ABC外部时,作CM⊥AB于M,由等腰直角三角形的性质得出∠ACD=∠1,由三角形的外角性质得出∠APC-∠ACD=90°;即可得出结论;
(2)延长CD至F,使DF=CD,则PD垂直平分CF,由线段垂直平分线的性质得出PF=PC,证出∠CPF=90°,点D是△PCF的外接圆圆心,证出点A、F、P、C四点共圆,得出DA=DP即可;
(3)作DG⊥BC于G,DH⊥AC于H,由垂径定理和矩形的性质得出DG=CH=$\frac{1}{2}$AC,由等腰直角三角形的性质得出AC=BC=$\frac{\sqrt{2}}{2}$AB=$\sqrt{3}$,得出DG=$\frac{\sqrt{3}}{2}$,由三角形面积公式即可得出结果.
解答 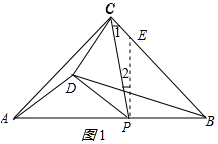 解:(1)∠APC+∠ACD=90°或∠APC-∠ACD=90°,理由如下:
解:(1)∠APC+∠ACD=90°或∠APC-∠ACD=90°,理由如下:
①点D在△ABC内部时,作PE⊥AB交BC于E,如图1所示:
∵△ABC和△CPD是等腰直角三角形,
∴∠ABC=∠BAC═∠DCP=∠DPC=45°,
∴△PBE是等腰直角三角形,∠ACD+∠1=90°-45°=45°,
∴∠BEP=45°,
∴∠1+∠2=45°,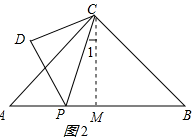
∴∠ACD=∠2,
∵∠2+∠APC=90°,
∴∠ACD+∠APC=90°;
故答案为:∠APC+∠ACD=90°或∠APC-∠ACD=90°;
②当点D在△ABC外部时,如图2所示:
作CM⊥AB于M,则∠ACM=45°,
∵∠DCP=45°,
∴∠ACD=∠1,
∵∠APC=90°+∠1,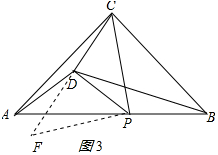
∴∠APC-∠ACD=90°;
(2)△ADP是等腰三角形,理由如下:
延长CD至F,使DF=CD,连接PF,如图3所示:
∵∠PDC=90°,
∴PD垂直平分CF,
∴PF=PC,
∴∠F=∠PCD=45°,∠FPD=∠DPC=45°,
∴∠CPF=90°,
∴点D是△PCF的外接圆圆心,
∵∠BAC=∠F=45°,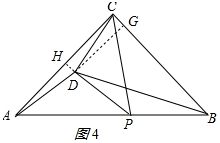
∴点A、F、P、C四点共圆,
∴DA=DP,即△ADP是等腰三角形;
(3)作DG⊥BC于G,DH⊥AC于H,如图4所示:
则CH=AH=$\frac{1}{2}$AC,四边形DHCG是矩形,
∴DG=CH=$\frac{1}{2}$AC,
∵△ABC是等腰直角三角形,AB=$\sqrt{6}$,
∴AC=BC=$\frac{\sqrt{2}}{2}$AB=$\sqrt{3}$,
∴DG=$\frac{\sqrt{3}}{2}$,
∴S△BCD=$\frac{1}{2}$BC•DG=$\frac{1}{2}$×$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{4}$.
点评 本题是三角形综合题目,考查了等腰直角三角形的判定与性质、线段垂直平分线的性质、四点共圆、垂径定理、矩形的判定、分类讨论等知识;本题综合性强,难度较大,需要通过作辅助线证明三角形是等腰直角三角形和证明四点共圆才能得出结论.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
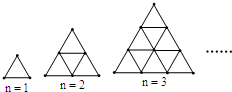 如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20(n=20)根时,需火柴棍为630 根,若当每边摆上n根时,试写出需火柴棍为$\frac{3n(1+n)}{2}$ 根.
如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20(n=20)根时,需火柴棍为630 根,若当每边摆上n根时,试写出需火柴棍为$\frac{3n(1+n)}{2}$ 根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
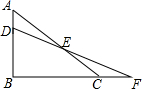 已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.
已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
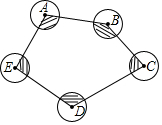 如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.
如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com