
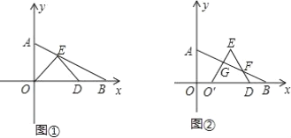
【题目】如图,在Rt△AOB中,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.
(1)如图①当E点恰好落在线段AB上时,求E点坐标;
(2)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,当E点到达△AOB的外面,且点D在点B左侧时,写出y与x的函数关系式,并写出自变量x的取值范围;
(3)在(1)问的条件下,将△ODE在线段OB上向右平移如图②,图中是否存在一条与线段OO′始终相等的线段?如果存在,请直接指出这条线段;如果不存在,请说明理由.
【答案】(1)E(1,![]() );(2)y=﹣
);(2)y=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() (2<x<4);(3)存在线段EF=OO';理由见解析
(2<x<4);(3)存在线段EF=OO';理由见解析
【解析】
(1)根据题意,作EH⊥OB于点H,由BO=4,求得OE,然后求出OH,EH,从而得出点E的坐标;
(2)根据题意,当E点到达△AOB的外面,且点D在点B左侧时,2<x<4即可;
(3)假设存在,由OO′=4﹣2﹣DB,而DF=DB,从而得到EF=OO'.
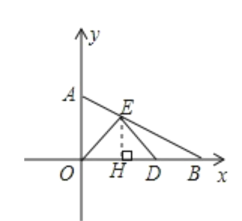
解:(1)作EH⊥OB于点H,
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=![]() OB=2.
OB=2.
∵△OEH是直角三角形,且∠OEH=30°,
∴OH=![]() OE=1,EH=
OE=1,EH=![]() ,
,
∵点E在第一象限内,
∴E(1,![]() ),
),
故答案为:E(1,![]() );
);
(2)当2<x<4,符合题意,如图,
由(1)知∠OEB=90°,∠E′=60°,
所求重叠部分四边形OD′NE的面积为:
S△OD′E′﹣S△E′EN=![]() OD×EH﹣
OD×EH﹣![]() E′E×EN=
E′E×EN=![]() x2﹣
x2﹣![]() ×
×![]() (x﹣2)=﹣
(x﹣2)=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]()
∴y=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() (2<x<4),
(2<x<4),
故答案为:y=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() (2<x<4);
(2<x<4);
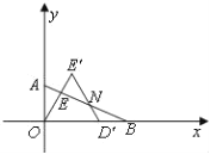
(3)存在线段EF=OO'.
∵∠ABO=30°,∠EDO=60°,
∴∠ABO=∠DFB=30°,
∴DF=DB,
∴OO′=4﹣2﹣DB=2﹣DB=2﹣DF=ED﹣DF=EF,
故答案为:存在线段EF=OO'.


科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
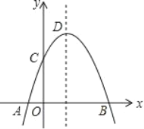
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=3;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .
.
其中真命题的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
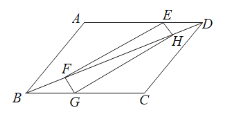
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
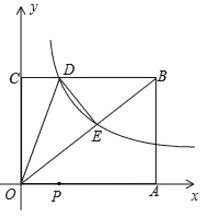
【题目】如图,已知矩形![]() 的两边OA,OC分别落在
的两边OA,OC分别落在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() 的中点E,且与BC边相交于点D.
的中点E,且与BC边相交于点D.
(1)①求反比例函数的解析式及点D的坐标;
②直接写出![]() 的面积为________.
的面积为________.
(2)若P是OA上的动点,当![]() 值为最小时,求直线
值为最小时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
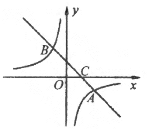
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)将![]() 轴下方的图像沿
轴下方的图像沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据北京市统计局发布的统计数据显示,北京市近五年国民生产总值数据如图1所示,2017年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示,根据以上信息,下列判断错误的是( )
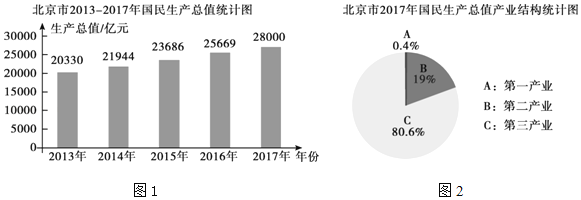
A.2013年至2017年北京市国民生产总值逐年增加
B.2017年第二产业生产总值为5 320亿元
C.2017年比2016年的国民生产总值增加了10%
D.若从2018年开始,每一年的国民生产总值比前一年均增长10%,到2019年的国民生产总值将达到33 880亿元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com