
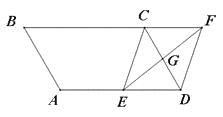
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
【答案】(1)证明见解析;
(2)① 当AE=3.5cm时,四边形CEDF是矩形.
② 当AE=2cm时,四边形CEDF是菱形.
【解析】
试题(1)利用“ASA”即可得证;
①当四边形CEDF是矩形时,则有EG=DG=1.5cm,又由已知可得∠ADC=60°,从而得△EGD为等边三角形,从而得DE=1.5cm,从而得AE=3.5cm;
②.当四边形CEDF是菱形时,则有EF⊥CD,由已知可知∠ADC=60°,从而可得∠DEG=30°,从而得DE=2DG=3,从而得AE=2.
试题解析:(1)∵ 四边形ABCD是平行四边形, ∴ CF∥ED, ∴ ∠FCG=∠EDG,∵ G是CD的中点,∴ CG=DG,在△FCG和△EDG中,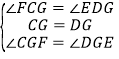 ,∴ △FCG ≌△EDG(ASA),∴ FG=EG,∵ CG=DG,∴ 四边形CEDF是平行四边形;
,∴ △FCG ≌△EDG(ASA),∴ FG=EG,∵ CG=DG,∴ 四边形CEDF是平行四边形;
(2)① 当AE=3.5cm时,四边形CEDF是矩形.
② 当AE=2cm时,四边形CEDF是菱形.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,BC=2,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C'.
(1)如果C'落在线段AB的延长线上.
①在图①中补全图形;
②求线段BP的长度;
(2)如图②,设直线AP与CC'的交点为M,求证:BM⊥DM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=8cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为
1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:

(1)当t为何值时,PE∥AB?
(2)是否存在某一时刻t,使S△DEQ=![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
(3)如图2连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
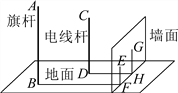
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足![]() ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com