
 20、如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE.请写出正确结论的序号
20、如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE.请写出正确结论的序号

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
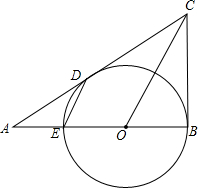 如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.
如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.查看答案和解析>>
科目:初中数学 来源:2010-2011学年广西柳州市启智中学九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2013年江苏省南通市海门市中考数学调研试卷(解析版) 题型:解答题
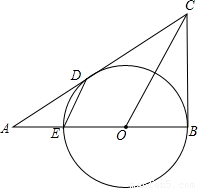
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《相交线与平行线》(02)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com