
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
【答案】∠2=∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;
∠AGD;两直线平行,同旁内角互补;105°;
【解析】试题分析:先根据两直线平行同位角相等可得∠2=∠3,然后根据等量代换可得∠1=∠3,然后根据内错角相等两直线平行可得AB∥DG,然后根据两直线平行同旁内角互补可得∠BAC+∠AGD=180°,进而可求∠AGD的度数.
试题解析:∵EF∥AD(已知)
∴∠2=∠3(两直线平行同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等两直线平行)
∴∠BAC+∠AGD=180°(两直线平行同旁内角互补)
∵∠BAC=75°(已知)
∴∠AGD=105°.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】2017年中秋、国庆假日八天里,中国民航共运送旅客1295万人次,将1295万用科学记数法表示应为( )
A. 0.1295 108 B. 1295104 C. 12.95 106 D. 1.295107
查看答案和解析>>
科目:初中数学 来源: 题型:
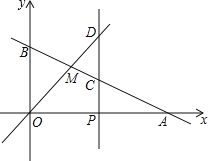
【题目】如图,已知函数y=﹣![]() x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.
x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.
(1)分别求出点A、点M的坐标;
(2)在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣![]() x+3和y=x的图象于点C、D,且OB=2CD,求a的值.
x+3和y=x的图象于点C、D,且OB=2CD,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
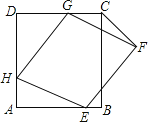
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为______.
,AB=2,则图中阴影部分的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a0+2b1﹣1=2b﹣1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com