
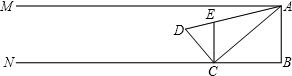
 AC,过C作CE⊥BN交AD于点E,设BC长为t.
AC,过C作CE⊥BN交AD于点E,设BC长为t. AC,根据三角形面的求解方法即可求得△ACD的面积;
AC,根据三角形面的求解方法即可求得△ACD的面积; AD,②当AE=AC时,AM⊥DF,③当0≤t<12时,∠AEC为钝角,故AC≠CE,当t≥12时,CE≤DF<DC<AC去分析求解,即可得到当BC等于
AD,②当AE=AC时,AM⊥DF,③当0≤t<12时,∠AEC为钝角,故AC≠CE,当t≥12时,CE≤DF<DC<AC去分析求解,即可得到当BC等于 和6+3
和6+3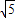 时,△ACE为等腰三角形.
时,△ACE为等腰三角形. 解:(1)∵AB⊥BN,
解:(1)∵AB⊥BN,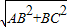 =
=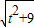 ;
; AC=
AC=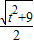 ,
, AC•CD=
AC•CD= ×
×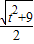 ×
×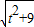 =
=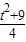 ;
;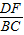 =
=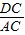 =
= ,
, ,BC=t.
,BC=t. ;
; AD,
AD, ;
;
 AC,
AC, 时,△ACE为等腰三角形.
时,△ACE为等腰三角形.

科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2009年江苏省南京市鼓楼区中考数学一模试卷(解析版) 题型:解答题
 AC,过C作CE⊥BN交AD于点E,设BC长为t.
AC,过C作CE⊥BN交AD于点E,设BC长为t.查看答案和解析>>
科目:初中数学 来源:2012年山东省临沂市中考数学模拟试卷(八)(解析版) 题型:解答题
 AC,过C作CE⊥BN交AD于点E,设BC长为t.
AC,过C作CE⊥BN交AD于点E,设BC长为t.查看答案和解析>>
科目:初中数学 来源:2011年江苏省南京市鼓楼区中考数学一模试卷(解析版) 题型:解答题
 AC,过C作CE⊥BN交AD于点E,设BC长为t.
AC,过C作CE⊥BN交AD于点E,设BC长为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com