
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法,下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.
问题情境:在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() .以
.以![]() 为旋转中心,将线段
为旋转中心,将线段![]() 顺时针旋转,旋转角与
顺时针旋转,旋转角与![]() 相等,得到线段
相等,得到线段![]() ,连接
,连接![]() .
.
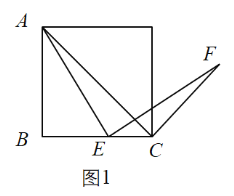
(1)特例如图1,若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 位置关系是_________.此时可以过点
位置关系是_________.此时可以过点![]() 作
作![]() 的平行线来对结论进行证明(这里不要求证明)
的平行线来对结论进行证明(这里不要求证明)
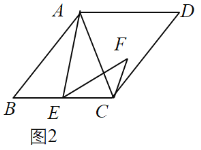
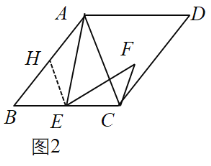
(2)拓展探究:如图2,若四边形![]() 是菱形,当
是菱形,当![]() 时,求
时,求![]() 的度数;
的度数;
【答案】(1)![]() ;(2)50°.
;(2)50°.
【解析】
(1)如图1中,作EH∥AC交AB于H.只要证明△HAE≌△CEF,即可推出∠AHE=∠ECF=135°,由∠BCA=45°,推出∠ACF=90°;
(2)如图2中,作EH∥AC交AB于H.只要证明△HAE≌△CEF,即可解决问题.
解:(1)证明:如图1中,作EH∥AC交AB于H.
∵四边形ABCD是正方形,
∴AB=BC,∠BAC=∠BCA=45°,
∵EH∥AC,
∴∠BHE=∠BAC=45°,∠BEH=∠BCA=45°,
∴∠BHE=∠BEH=45°,∠AHE=135°,
∴BH=BE, ∴AH=CE,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∵∠AEF=∠B=90°,
∴∠HAE=∠CEF,
在△HAE和△CEF中,

∴△HAE≌△CEF,
∴∠AHE=∠ECF=135°,
∵∠BCA=45°,
∴∠ACF=90°,
∴AC⊥CF.
故答案为:AC⊥CF.
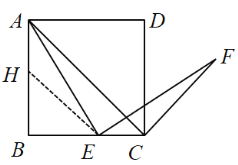
(2)如图2中,过点E作EH∥AC交AB于H.
∵四边形ABCD是菱形,
∴AB=BC,∠BAC=∠BCA,
∵EH∥AC,
∴∠BHE=∠BAC,∠BEH=∠BCA,
∴∠BHE=∠BEH,
∴BH=BE,
∴AH=CE,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∵∠AEF=∠B,
∴∠HAE=∠CEF,
在△HAE和△CEF中,
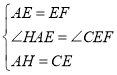 ,
,
∴△HAE≌△CEF,
∴∠AHE=∠ECF,
∵∠B=50°,
∴∠BHE=![]() ∠ACB=65°,
∠ACB=65°,
∴∠AHE=∠ECF=115°
∴∠ACF=115°﹣65°=50°.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
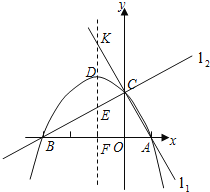
【题目】已知两直线l1,l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1,抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
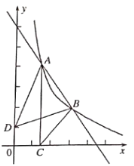
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
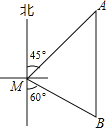
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时).(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月16日扬州首批为民服务5G站点正式上线,自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
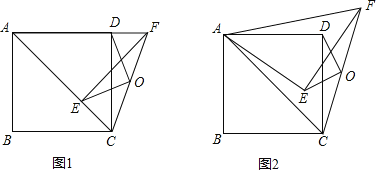
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所研发了一种新药,试验药效时发现:1.5小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax2+bx表示;1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=![]() (k>0)表示,部分实验数据如表:
(k>0)表示,部分实验数据如表:
时间x(小时) | 0.2 | 1 | 1.8 | … |
含药量y(微克) | 7.2 | 20 | 12.5 | … |
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(![]() ≈1.41,精确到0.1小时)
≈1.41,精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
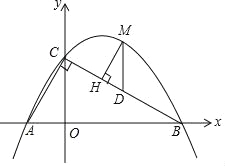
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com