
分析 (1)由和谐三组数的定义进行验证即可;
(2)把M、N、R三点的坐标分别代入反比例函数解析式,可用t和k分别表示出y1、y2、y3,再由和谐三组数的定义可得到关于t的方程,可求得t的值;
(3)①由直线解析式可求得x1=-$\frac{c}{b}$,联立直线和抛物线解析式消去y,利用一元二次方程根与系数的关系可求得x2+x3=-$\frac{b}{a}$,x2x3=$\frac{c}{a}$,再利用和谐三数组的定义证明即可;②由条件可得到a+b+c=0,可得c=-(a+b),由a>2b>3c可求得$\frac{b}{a}$的取值范围,令m=$\frac{b}{a}$,利用两点间距离公式可得到OP2关于m的二次函数,利用二次函数的性质可求得OP2的取值范围,从而可求得OP的取值范围.
解答 解:
(1)不能,理由如下:
∵1、2、3的倒数分别为1、$\frac{1}{2}$、$\frac{1}{3}$,
∴$\frac{1}{2}$+$\frac{1}{3}$≠1,1+$\frac{1}{2}$≠$\frac{1}{3}$,1+$\frac{1}{3}$≠$\frac{1}{2}$
∴实数1,2,3不可以构成“和谐三组数”;
(2)∵M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数$\frac{k}{x}$(k为常数,k≠0)的图象上,
∴y1、y2、y3均不为0,且y1=$\frac{k}{t}$,y2=$\frac{k}{t+1}$,y3=$\frac{k}{t+3}$,
∴$\frac{1}{{y}_{1}}$=$\frac{t}{k}$,$\frac{1}{{y}_{2}}$=$\frac{t+1}{k}$,$\frac{1}{{y}_{3}}$=$\frac{t+3}{k}$,
∵y1,y2,y3构成“和谐三组数”,
∴有以下三种情况:
当$\frac{1}{{y}_{1}}$=$\frac{1}{{y}_{2}}$+$\frac{1}{{y}_{3}}$时,则$\frac{t}{k}$=$\frac{t+1}{k}$+$\frac{t+3}{k}$,即t=t+1+t+3,解得t=-4;
当$\frac{1}{{y}_{2}}$=$\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{3}}$时,则$\frac{t+1}{k}$=$\frac{t}{k}$+$\frac{t+3}{k}$,即t+1=t+t+3,解得t=-2;
当$\frac{1}{{y}_{3}}$=$\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{2}}$时,则$\frac{t+3}{k}$=$\frac{t}{k}$+$\frac{t+1}{k}$,即t+3=t+t+1,解得t=2;
∴t的值为-4、-2或2;
(3)①∵a、b、c均不为0,
∴x1,x2,x3都不为0,
∵直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),
∴0=2bx1+2c,解得x1=-$\frac{c}{b}$,
联立直线与抛物线解析式,消去y可得2bx+2c=ax2+3bx+3c,即ax2+bx+c=0,
∵直线与抛物线交与B(x2,y2),C(x3,y3)两点,
∴x2、x3是方程ax2+bx+c=0的两根,
∴x2+x3=-$\frac{b}{a}$,x2x3=$\frac{c}{a}$,
∴$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$=$\frac{{x}_{2}+{x}_{3}}{{x}_{2}{x}_{3}}$=$\frac{-\frac{b}{a}}{\frac{c}{a}}$=-$\frac{b}{c}$=$\frac{1}{{x}_{1}}$,
∴x1,x2,x3构成“和谐三组数”;
②∵x2=1,
∴a+b+c=0,
∴c=-a-b,
∵a>2b>3c,
∴a>2b>3(-a-b),且a>0,整理可得$\left\{\begin{array}{l}{a>2b}\\{5b>-3a}\end{array}\right.$,解得-$\frac{3}{5}$<$\frac{b}{a}$<$\frac{1}{2}$,
∵P($\frac{c}{a}$,$\frac{b}{a}$)
∴OP2=($\frac{c}{a}$)2+($\frac{b}{a}$)2=($\frac{-a-b}{a}$)2+($\frac{b}{a}$)2=2($\frac{b}{a}$)2+2$\frac{b}{a}$+1=2($\frac{b}{a}$+$\frac{1}{2}$)2+$\frac{1}{2}$,
令m=$\frac{b}{a}$,则-$\frac{3}{5}$<m<$\frac{1}{2}$且m≠0,且OP2=2(m+$\frac{1}{2}$)2+$\frac{1}{2}$,
∵2>0,
∴当-$\frac{3}{5}$<m<-$\frac{1}{2}$时,OP2随m的增大而减小,当m=-$\frac{3}{5}$时,OP2有最大值$\frac{26}{50}$,当m=-$\frac{1}{2}$时,OP2有最小值$\frac{1}{2}$,
当-$\frac{1}{2}$<m<$\frac{1}{2}$时,OP2随m的增大而增大,当m=-$\frac{1}{2}$时,OP2有最小值$\frac{1}{2}$,当m=$\frac{1}{2}$时,OP2有最大值$\frac{5}{2}$,
∴$\frac{1}{2}$≤OP2<$\frac{5}{2}$且OP2≠1,
∵P到原点的距离为非负数,
∴$\frac{\sqrt{2}}{2}$≤OP<$\frac{\sqrt{10}}{2}$且OP≠1.
点评 本题为二次函数的综合应用,涉及新定义、函数图象的交点、一元二次方程根与系数的关系、勾股定理、二次函数的性质、分类讨论思想及转化思想等知识.在(1)中注意利用和谐三数组的定义,在(2)中由和谐三数组得到关于t的方程是解题的关键,在(3)①中用a、b、c分别表示出x1,x2,x3是解题的关键,在(3)②中把OP2表示成二次函数的形式是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,难度很大.


科目:初中数学 来源: 题型:选择题
| A. | 74.4×1012 | B. | 7.44×1012 | C. | 0.744×1013 | D. | 7.44×1013 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件A和B都是随机事件 | B. | 只有事件B是随机事件 | ||
| C. | 只有事件A是随机事件 | D. | 事件A和B都不是随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
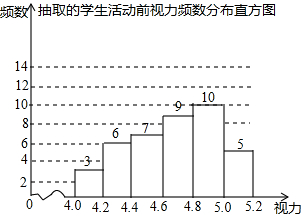 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示 | 分组 | 频数 |
| 4.0≤x<4.2 | 2 |
| 4.2≤x<4.4 | 3 |
| 4.4≤x<4.6 | 5 |
| 4.6≤x<4.8 | 8 |
| 4.8≤x<5.0 | 17 |
| 5.0≤x<5.2 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | -8 | C. | $\frac{1}{16}$ | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
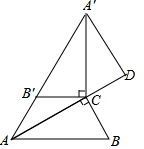 如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
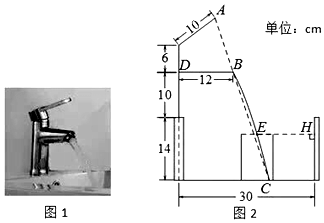
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{9}{8}$ | B. | m$>\frac{8}{9}$ | C. | m=$\frac{9}{8}$ | D. | m=$\frac{8}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com