
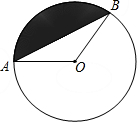
 如图,在⊙O中,弦AB所对的劣弧是圆周长的$\frac{1}{3}$,其中圆的半径为4cm,求:
如图,在⊙O中,弦AB所对的劣弧是圆周长的$\frac{1}{3}$,其中圆的半径为4cm,求:分析 (1)要求AB的长,只要作OC⊥AB于点C,然后根据勾股定理即可解答本题;
(2)由图可知,阴影部分的面积是扇形的面积与三角形的面积之差.
解答 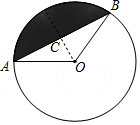 解:(1)作OC⊥AB于点C,如右图所示,
解:(1)作OC⊥AB于点C,如右图所示,
∵在⊙O中,弦AB所对的劣弧是圆周长的$\frac{1}{3}$,其中圆的半径为4cm,
∴∠AOB=120°,
∴∠AOC=60°,∠OAC=30°,
∴OC=2cm,
∴AC=2$\sqrt{3}$cm,
∴AB=4$\sqrt{3}$cm;
(2)∵OC=2cm,AB=4$\sqrt{3}$cm,∠AOB=120°,OA=4cm,
∴阴影部分的面积是:$\frac{120×π×{4}^{2}}{360}-\frac{4\sqrt{3}×2}{2}$=($\frac{16π}{3}-4\sqrt{3}$)cm2.
点评 本题考查扇形面积的计算、勾股定理,解题的关键是明确题意,找出所求问题需要的条件.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区七年级3月教学质量检测数学试卷(解析版) 题型:填空题
某书店把一本新书按标价的八折出售,仍可获利20%,若该书的进价为20元,则标价为___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
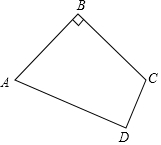 如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com