
【题目】如图,反比例函数y= ![]() (x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则
(x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则 ![]() = , 当k=4时,四边形ODBE的面积为平方单位.
= , 当k=4时,四边形ODBE的面积为平方单位. 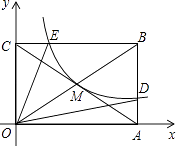
【答案】![]() ;12
;12
【解析】解:设B(a,b), ∴E( ![]() ,b),D(a,
,b),D(a, ![]() ),M(
),M( ![]() a,
a, ![]() b),
b),
∴k= ![]() a
a ![]() b=
b= ![]() ,
,
∴ab=4k,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
∵E、M、D位于反比例函数图象上,
则S△OCE= ![]() =2,S△OAD=
=2,S△OAD= ![]() =2,
=2,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=k,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4k=16,
∴2+2+S四边形ODBE=16,
解得:S四边形ODBE=12.
所以答案是 ![]() ;12.
;12.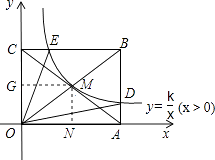
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


科目:初中数学 来源: 题型:
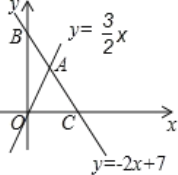
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元. 
(1)求W关于x的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可节约多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分别是AE,CD的中点.
(1)求证:△ABM≌△DBN;
(2)试探索BM和BN的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售公司为了提高员工的工作积极性,对员工的工资结构进行改革,改革后月工资由基本保障工资与计件奖励工资组成.(计件奖励工资=销售每件的奖励金额×销售的件数)下表是甲、乙两位职工今年三月份的工资情况信息:
职工 | 甲 | 乙 |
月销售件数(件) | 100 | 80 |
月工资(元) | 4500 | 4100 |
求员工的月基本保障工资和销售每件产品的奖励金额各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.若Rt△ABC为匀称三角形,且∠C=90°,AC=4,则BC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com