
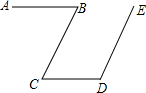
 如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.
如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.  状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
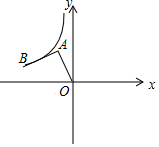 如图,在平面直角坐标系中,点A(-1,2),将AO绕点A顺时针旋转90°,点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上,则k的值为-3.
如图,在平面直角坐标系中,点A(-1,2),将AO绕点A顺时针旋转90°,点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上,则k的值为-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请你给如图建立平面直角坐标系,使文化宫的坐标为(-3,1),超市的坐标为(2,-3).
请你给如图建立平面直角坐标系,使文化宫的坐标为(-3,1),超市的坐标为(2,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com