练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

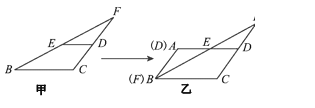
    【题目】如图甲，已知ED是△FBC的中位线，沿线段ED将△FED剪下后拼接在图乙中△BEA的位置．

    （1）从△FED到△BEA的图形变换，可以认为是（填平移或轴对称或旋转）变换；

    （2）试判断图乙中四边形ABCD的形状，并证明你的结论．

    【答案】（1）旋转变换；（2）四边形ABCD是平行四边形，见解析

    【解析】

    （1）由拼接后发现对应点分别是为B与F，A与D，E与E，所以可以得到答案．

    （2）利用旋转的性质得到ED=EA，结合中位线的性质得到AD∥BC，AD=BC可以得出结论．

    解：(1)拼接后，B与F是对应点，A与D是对应点，E与自身对应，所以是旋转对称关系，即旋转变换.

    (2)四边形ABCD是平行四边形

    证明:∵△FED到△BEA是旋转变换,

    ∴ED=EA.∴AD=2ED.

    ∵ED是△FBC的中位线,

    ∴ED∥CB，CB=2DE,

    ∴AD∥BC，AD=BC.

    ∴四边形ABCD是平行四边形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，⊙O过正方形ABCD的顶点A、D且与边BC相切于点E，分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x，圆心O与P点的距离为y，图2记录了一段时间里y与x的函数关系，在这段时间里P点的运动路径为（ ）

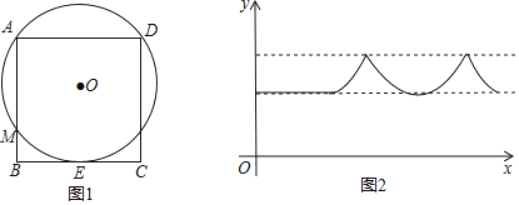
    A. 从D点出发，沿弧DA→弧AM→线段BM→线段BC

    B. 从B点出发，沿线段BC→线段CN→弧ND→弧DA

    C. 从A点出发，沿弧AM→线段BM→线段BC→线段CN

    D. 从C点出发，沿线段CN→弧ND→弧DA→线段AB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

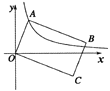
    【题目】如图，已知点是反比例函数在第一象限图像上的一个动点，连接，以 为长，为宽作矩形，且点在第四象限，随着点的运动，点也随之运动，但点始终在反比例函数的图像上，则的值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

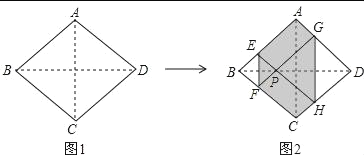
    【题目】如图1，正方形纸片ABCD边长为2，折叠∠B和∠D，使两个直角的顶点重合于对角线BD上的一点P，EF、GH分别是折痕（图2），设AE=x（0＜x＜2），给出下列判断：①x=时，EF+AB＞AC；②六边形AEFCHG周长的值为定值；③六边形AEFCHG面积为定值，其中正确的是（　　）

    A.①②B.①③C.②D.②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线L：y=﹣x+2与x轴、y轴分别交于A、B两点，在y轴上有一点N（0，4），动点M从A点以每秒1个单位的速度匀速沿x轴向左移动．

    （1）点A的坐标：_____；点B的坐标：_____；

    （2）求△NOM的面积S与M的移动时间t之间的函数关系式；

    （3）在y轴右边，当t为何值时，△NOM≌△AOB，求出此时点M的坐标；

    （4）在（3）的条件下，若点G是线段ON上一点，连结MG，△MGN沿MG折叠，点N恰好落在x轴上的点H处，求点G的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠ABC=30°，∠ADC=60°，AD=DC．

    （操作）（1）将△ABD绕点D沿顺时针方向旋转60°，在图中画出旋转后的三角形．

    （探究）（2）结合所画图形探究BD与AB，BC之间的数量关系，并证明你的结论．

    （应用）（3）若AB=6，BC=8，试求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED=45°．

    （1）判断CD与⊙O的位置关系，并说明理由；

    （2）若⊙O半径为4cm，AE=6cm，求∠ADE的正切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 已知∠BAC=36°，△A1B1A2，△A2B2A3，△A3B3A4，…，△AnBnAn+1都是顶角为36°的等腰三角形，即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°，点A1，A2，A3，…，An在射线AC上，点B1，B2，B3，…，Bn在射线AB上，若A1A2=1，则线段A2018A2019的长为______．

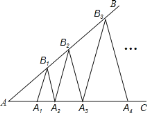
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，AB＝2，点E是CD的中点，连接AE，将△ADE沿AE折叠至△AHE，连接BH，延长AE，BH交于点F；BF，CD交于点G，则FG=_______．

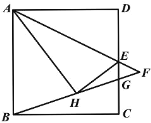
    查看答案和解析>>

    同步练习册答案