
ЎѕМвДїЎїДіѕ°µгКФїЄ·ЕЖЪјдЈ¬НЕ¶УКХ·С·Ѕ°ёИзПВЈєІ»і¬№э30ИЛК±Ј¬ИЛѕщКХ·С120ФЄЈ»і¬№э30ИЛЗТІ»і¬№эmЈЁ30ЈјmЎЬ100Ј©ИЛК±Ј¬ГїФцјУ1ИЛЈ¬ИЛѕщКХ·СЅµµН1ФЄЈ»і¬№эmИЛК±Ј¬ИЛѕщКХ·С¶ј°ґХХmИЛК±µД±кЧјЈ®Йиѕ°µгЅУґэУРxГыУОїНµДДіНЕ¶УЈ¬КХИЎЧЬ·СУГОЄyФЄЈ®
ЈЁ1Ј©Зуy№ШУЪxµДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©ѕ°µг№¤ЧчИЛФ±·ўПЦЈєµ±ЅУґэДіНЕ¶УИЛКэі¬№эТ»¶ЁКэБїК±Ј¬»біцПЦЛжЧЕИЛКэµДФцјУКХИЎµДЧЬ·СУГ·ґ¶шјхЙЩХвТ»ПЦПуЈ®ОЄБЛИГКХИЎµДЧЬ·СУГЛжЧЕНЕ¶УЦРИЛКэµДФцјУ¶шФцјУЈ¬ЗуmµДИЎЦµ·¶О§Ј®
Ўѕґр°ёЎїЈЁ1Ј©y=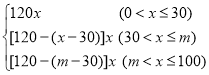 Ј»ЈЁ2Ј©30ЈјmЎЬ75Ј®
Ј»ЈЁ2Ј©30ЈјmЎЬ75Ј®
ЎѕЅвОцЎї
КФМв·ЦОцЈєЈЁ1Ј©ёщѕЭКХ·С±кЧјЈ¬·Ц0ЈјxЎЬ30Ј¬30ЈјxЎЬmЈ¬mЈјxЎЬ100·Ц±рЗуіцyУлxµД№ШПµјґїЙЈ®
ЈЁ2Ј©УЙЈЁ1Ј©їЙЦЄµ±0ЈјxЎЬ30»тmЈјxЈј100Ј¬єЇКэЦµy¶јКЗЛжЧЕxКЗФцјУ¶шФцјУЈ¬30ЈјxЎЬmК±Ј¬![]() Ј¬ёщѕЭ¶юґОєЇКэµДРФЦКјґїЙЅвѕцОКМвЈ®
Ј¬ёщѕЭ¶юґОєЇКэµДРФЦКјґїЙЅвѕцОКМвЈ®
КФМвЅвОцЈєЈЁ1Ј©y=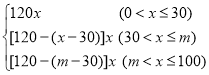 Ј®
Ј®
ЈЁ2Ј©УЙЈЁ1Ј©їЙЦЄµ±0ЈјxЎЬ30»тmЈјxЈј100Ј¬єЇКэЦµy¶јКЗЛжЧЕxКЗФцјУ¶шФцјУЈ¬µ±30ЈјxЎЬmК±Ј¬![]() Ј¬ЎЯa=©Ѓ1Јј0Ј¬ЎаxЎЬ75К±Ј¬yЛжЧЕxФцјУ¶шФцјУЈ¬ЎаОЄБЛИГКХИЎµДЧЬ·СУГЛжЧЕНЕ¶УЦРИЛКэµДФцјУ¶шФцјУЈ¬Ўа30ЈјmЎЬ75Ј®
Ј¬ЎЯa=©Ѓ1Јј0Ј¬ЎаxЎЬ75К±Ј¬yЛжЧЕxФцјУ¶шФцјУЈ¬ЎаОЄБЛИГКХИЎµДЧЬ·СУГЛжЧЕНЕ¶УЦРИЛКэµДФцјУ¶шФцјУЈ¬Ўа30ЈјmЎЬ75Ј®


 ДЬБ¦ЖАјЫПµБРґр°ё
ДЬБ¦ЖАјЫПµБРґр°ё МЖУЎОД»ЇїОК±ІвЖАПµБРґр°ё
МЖУЎОД»ЇїОК±ІвЖАПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
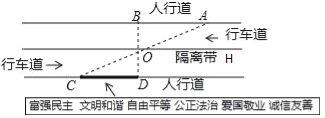
ЎѕМвДїЎїСоСфН¬С§СШТ»¶О±КЦ±µДИЛРРµАРРЧЯЈ¬ФЪУЙAІЅРРµЅґпBґ¦µД№эіМЦРЈ¬НЁ№эёфАлґшµДїХП¶OЈ¬ёХєГдЇААНк¶ФГжИЛРРµАРыґ«ЗЅЙПµДЙз»бЦчТеєЛРДјЫЦµ№Ы±кУпЈ¬ЖдѕЯМеРЕПў»гјЇИзПВЈє
ИзНјЈ¬ABЎОOHЎОCDЈ¬ПаБЪБЅЖЅРРПЯјдµДѕаАлПаµИЈ¬ACЈ¬BDПаЅ»УЪOЈ¬ODЎНCDЈ®ґ№ЧгОЄDЈ¬ТСЦЄAB=20ГЧЈ¬ЗлёщѕЭЙПКцРЕПўЗу±кУпCDµДі¤¶ИЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪјЧЎўТТБЅёцІ»НёГчµДІјґьАпЈ¬¶јЧ°УР3ёцґуРЎЎўІДЦКНкИ«ПаН¬µДРЎЗтЈ¬ЖдЦРјЧґьЦРµДРЎЗтЙП·Ц±р±кУРКэЧЦ0Ј¬1Ј¬2Ј»ТТґьЦРµДРЎЗтЙП·Ц±р±кУРКэЧЦ©Ѓ1Ј¬©Ѓ2Ј¬0Ј®ПЦґУјЧґьЦРИОТвГюіцТ»ёцРЎЗтЈ¬јЗЖд±кУРµДКэЧЦОЄxЈ¬ФЩґУТТґьЦРИОТвГюіцТ»ёцРЎЗтЈ¬јЗЖд±кУРµДКэЧЦОЄyЈ¬ТФґЛИ·¶ЁµгMµДЧш±кЈЁxЈ¬yЈ©Ј®
ЈЁ1Ј©ЗлДгУГ»КчЧґНј»тБР±нµД·Ѕ·ЁЈ¬РґіцµгMЛщУРїЙДЬµДЧш±кЈ»
ЈЁ2Ј©ЗуµгMЈЁxЈ¬yЈ©ФЪєЇКэ![]() µДНјПуЙПµДёЕВКЈ®
µДНјПуЙПµДёЕВКЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОДОДєН±т±тФЪЦ¤ГчЎ°УРБЅёцЅЗПаµИµДИэЅЗРОКЗµИСьИэЅЗРОЎ±ХвТ»ГьМвК±Ј¬»іцНјРОЈ¬РґіцЎ°ТСЦЄЎ±Ј¬Ў°ЗуЦ¤Ў±ЈЁИзНјЈ©Ј¬ЛэГЗ¶ФёчЧФЛщЧчµДёЁЦъПЯГиКцИзПВЈє
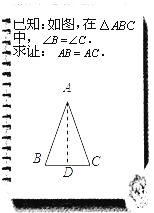
ОДОДЈєЎ°№эµгAЧчBCµДЦРґ№ПЯADЈ¬ґ№ЧгОЄDЎ±Ј»
±т±тЈєЎ°ЧчЎчABCµДЅЗЖЅ·ЦПЯADЎ±Ј®
КэС§АПК¦їґБЛБЅО»Н¬С§µДёЁЦъПЯЧч·ЁєуЈ¬ЛµЈєЎ°±т±тµДЧч·ЁКЗХэИ·µДЈ¬¶шОДОДµДЧч·ЁРиТЄ¶©ХэЈ®Ў±
ЈЁ1Ј©ЗлДгјтТЄЛµГчОДОДµДёЁЦъПЯЧч·ЁґнФЪДДАпЈ»
ЈЁ2Ј©ёщѕЭ±т±тµДёЁЦъПЯЧч·ЁЈ¬НкіЙЦ¤Гч№эіМЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИз№ыЅ«ЕЧОпПЯyЈЅЈЁx©Ѓ2Ј©2+1ПтЧуЖЅТЖ1ёцµҐО»Ј¬ФЩПтЙПЖЅТЖ3ёцµҐО»Ј¬ДЗГґЛщµГРВЕЧОпПЯµДЅвОцКЅОЄЈЁЎЎЎЎЈ©
A.yЈЅЈЁx©Ѓ3Ј©2+4B.yЈЅЈЁx©Ѓ1Ј©2+4C.yЈЅЈЁx+1Ј©2+2D.yЈЅЈЁx+1Ј©2
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЕЧОпПЯУлxЦбЅ»УЪAЈЁ6Ј¬0Ј©ЎўBЈЁ![]() Ј¬0Ј©БЅµгЈ¬УлyЦбЅ»УЪµгCЈ¬№эЕЧОпПЯЙПµгMЈЁ1Ј¬3Ј©ЧчMNЎНxЦбУЪµгNЈ¬Б¬ЅУOMЈ®
Ј¬0Ј©БЅµгЈ¬УлyЦбЅ»УЪµгCЈ¬№эЕЧОпПЯЙПµгMЈЁ1Ј¬3Ј©ЧчMNЎНxЦбУЪµгNЈ¬Б¬ЅУOMЈ®
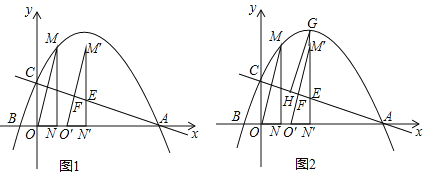
ЈЁ1Ј©ЗуґЛЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©ИзНј1Ј¬Ѕ«ЎчOMNСШxЦбПтУТЖЅТЖtёцµҐО»ЈЁ0ЎЬtЎЬ5Ј©µЅЎчOЎдMЎдNЎдµДО»ЦГЈ¬MNЎдЎўMЎдOЎдУлЦ±ПЯAC·Ц±рЅ»УЪµгEЎўFЈ®
ўЩµ±µгFОЄMЎдOЎдµДЦРµгК±Ј¬ЗуtµДЦµЈ»
ўЪИзНј2Ј¬ИфЦ±ПЯMЎдNЎдУлЕЧОпПЯПаЅ»УЪµгGЈ¬№эµгGЧчGHЎОMЎдOЎдЅ»ACУЪµгHЈ¬КФИ·¶ЁПЯ¶ОEHКЗ·сґжФЪЧоґуЦµЈїИфґжФЪЈ¬ЗуіцЛьµДЧоґуЦµј°ґЛК±tµДЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ЁТеЈєУРТ»Чй¶ФЅЗПаµИ¶шБнТ»Чй¶ФЅЗІ»ПаµИµДН№ЛД±ЯРОЅРЧцЎ°µИ¶ФЅЗЛД±ЯРОЎ±Ј®
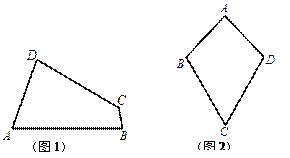
ЈЁ1Ј©ТСЦЄЈєИзНј1Ј¬ЛД±ЯРО![]() КЗЎ°µИ¶ФЅЗЛД±ЯРОЎ±Ј¬
КЗЎ°µИ¶ФЅЗЛД±ЯРОЎ±Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј®Зу
Ј®Зу![]() Ј¬
Ј¬ ![]() µД¶ИКэЈ®
µД¶ИКэЈ®
ЈЁ2Ј©ФЪМЅѕїЎ°µИ¶ФЅЗЛД±ЯРОЎ±РФЦКК±Јє
ўЩ РЎєм»БЛТ»ёцЎ°µИ¶ФЅЗЛД±ЯРОЎ±![]() ЈЁИзНј2Ј©Ј¬ЖдЦР
ЈЁИзНј2Ј©Ј¬ЖдЦР![]() Ј¬
Ј¬ ![]() Ј¬ґЛК±Лэ·ўПЦ
Ј¬ґЛК±Лэ·ўПЦ![]() іЙБўЈ®ЗлДгЦ¤ГчґЛЅбВЫЈ®
іЙБўЈ®ЗлДгЦ¤ГчґЛЅбВЫЈ®
ўЪ УЙґЛРЎємІВПлЈєЎ°¶ФУЪИОТвЎ®µИ¶ФЅЗЛД±ЯРОЎЇЈ¬µ±Т»ЧйБЪ±ЯПаµИК±Ј¬БнТ»ЧйБЪ±ЯТІПаµИЎ±Ј®ДгИПОЄЛэµДІВПлХэИ·ВрЈїИфХэИ·Ј¬ЗлЦ¤ГчЈ»ИфІ»ХэИ·Ј¬ЗлѕЩіц·ґАэЈ®
ЈЁ3Ј©ТСЦЄЈєФЪЎ°µИ¶ФЅЗЛД±ЯРОЎ±![]() ЦРЈ¬
ЦРЈ¬ ![]() Ј¬
Ј¬ ![]() Ј¬AB=AD=4Ј¬Ј®ЗуЎПDєН¶ФЅЗПЯ
Ј¬AB=AD=4Ј¬Ј®ЗуЎПDєН¶ФЅЗПЯ![]() µДі¤Ј®
µДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРјЖЛгХэИ·µДКЗЈЁ Ј©
A.a+a=2a
B.b3b3=2b3
C.a3ЎВa=a3
D.ЈЁa5Ј©2=a7
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com