
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
【答案】(1)侧面(2x+152)个,底面(190-5x)个;(2)60个.
【解析】
(1)由x张用A方法,可得有(38-x)张用B方法,就可以分别表示出侧面个数和底面个数;
(2)由侧面个数和底面个数比为3:2建立方程求出x的值,求出侧面的总数就可以求出结论.
解:(1)∵裁剪时x张用A方法,
∴裁剪时(38-x)张用B方法.
∴侧面的个数为:6x+4(38-x)=(2x+152)个,
底面的个数为:5(38-x)=(190-5x)个;
(2)由题意,得(2x+152):(190-5x)=3:2,
解得:x=14,
∴盒子的个数为:![]() .
.
答:裁剪出的侧面和底面恰好全部用完,能做60个盒子.
故答案为:(1)侧面(2x+152)个,底面(190-5x)个;(2)60个.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
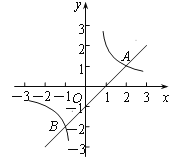
(1)求m及k的值;
(2)不解关于x、y的方程组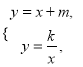 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 即可求得结果;
即可求得结果;
(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入![]() 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.
(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;
(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入![]() 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2
所以直线![]() 经过点B(-1,-2).
经过点B(-1,-2).
考点:反比例函数的性质
点评:反比例函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.
【题型】解答题
【结束】
20
【题目】某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
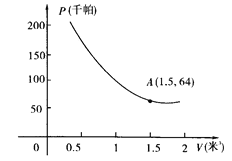
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕;
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:解不等式 ![]() .根据两数相除,同号得正,异号得负,得不等式组
.根据两数相除,同号得正,异号得负,得不等式组 ![]() 或不等式组
或不等式组![]() 解不等式组
解不等式组 ![]() ,得
,得 ![]() ;解不等式组
;解不等式组 ![]() ,得
,得 ![]() ,所以原不等式的解集为
,所以原不等式的解集为 ![]() 或
或![]() .
.
(1)探究:解不等式 ![]() .
.
(2)应用:不等式 ![]() 的解集是 .
的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都相同的四张卡片![]() ,
,![]() ,
,![]() ,
,![]() ,正面上分别写有四个实数
,正面上分别写有四个实数![]() ,
,![]() ,
,![]() ,
,![]() 将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)画树形图或列表法表示抽取两张卡片可能出现的所有情况(卡片可用![]() 、
、![]() 、
、![]() 、
、![]() 表示);
表示);
(2)求取到的两个数都是无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下题和解题过程:化简![]() ,使结果不含绝对值.
,使结果不含绝对值.
解:当![]() 时,即
时,即![]() 时,
时,
原式![]()
![]() ;
;
当![]() ,即
,即![]() 时,
时,
原式![]()
![]()
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:![]() ;
;
(2)试探究:当![]() 分别为何值时,方程
分别为何值时,方程![]()
①无解,②只有一个解,③有两个解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)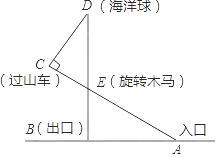
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:长方形ABCD中,点E为BC边的中点,将D折起,使点D落在点E处.

(1)请你用尺规作图画出折痕和折叠后的图形.(不要求写已知,求作和作法,保留作图痕迹)
(2)若折痕与AD、BC分别交于点M、N,与DE交于点O,求证△MDO≌△NEO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,把
,把![]() 的直角三角板
的直角三角板![]() 的直角顶点
的直角顶点![]() 放在直线
放在直线![]() 上.将直角三角板
上.将直角三角板![]() 在平面内绕点
在平面内绕点![]() 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线![]() 与直线
与直线![]() 的夹角为60°,则
的夹角为60°,则![]() 的度数为___.
的度数为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com