
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=3}\\{x-y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=-1}\\{x-y=-3}\end{array}\right.$ |
分析 把$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$代入各个方程组中,该解满足两个方程即为所求二元一次方程组.
解答 解:A、当$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$时,x+y=2-1=1,x-y=2+1=3,不符合题意;
B、当$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$时,x+y=2-1=1,x-y=2+1=3,符合题意;
C、当$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$时,x+y=2-1=1,x-y=2+1=3,不符合题意;
D、当$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$时,x+y=2-1=1,x-y=2+1=3,不符合题意;
故选:B.
点评 考查了二元一次方程组的解,一般情况下二元一次方程组的解是唯一的.数学概念是数学的基础与出发点,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.


科目:初中数学 来源: 题型:解答题
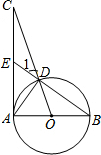 如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量/m3 | 水费/元 |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
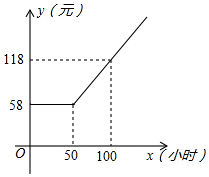 某广电局与长江证券公司联合推出光电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示.
某广电局与长江证券公司联合推出光电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
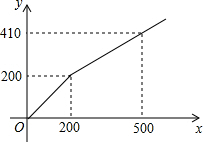 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )| A. | 打八折 | B. | 打七折 | C. | 打六折 | D. | 打五折 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com