
 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为$\frac{9}{4}$或1.
如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为$\frac{9}{4}$或1. 分析 分两种情况进行讨论:当∠CFE=90°时,△ECF是直角三角形;当∠CEF=90°时,△ECF是直角三角形,分别根据直角三角形的勾股定理列方程求解即可.
解答 解:如图所示,当∠CFE=90°时,△ECF是直角三角形,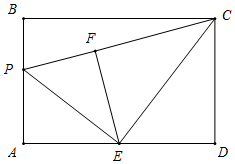
由折叠可得,∠PFE=∠A=90°,AE=FE=DE,
∴∠CFP=180°,即点P,F,C在一条直线上,
在Rt△CDE和Rt△CFE中,
$\left\{\begin{array}{l}{CE=CE}\\{EF=ED}\end{array}\right.$,
∴Rt△CDE≌Rt△CFE(HL),
∴CF=CD=4,
设AP=FP=x,则BP=4-x,CP=x+4,
在Rt△BCP中,BP2+BC2=PC2,即(4-x)2+62=(x+4)2,
解得x=$\frac{9}{4}$,即AP=$\frac{9}{4}$;
如图所示,当∠CEF=90°时,△ECF是直角三角形,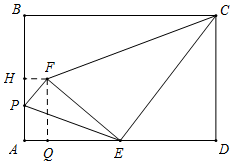
过F作FH⊥AB于H,作FQ⊥AD于Q,则∠FQE=∠D=90°,
又∵∠FEQ+∠CED=90°=∠ECD+∠CED,
∴∠FEQ=∠ECD,
∴△FEQ∽△ECD,
∴$\frac{FQ}{ED}$=$\frac{QE}{DC}$=$\frac{EF}{CE}$,即$\frac{FQ}{3}$=$\frac{QE}{4}$=$\frac{3}{5}$,
解得FQ=$\frac{9}{5}$,QE=$\frac{12}{5}$,
∴AQ=HF=$\frac{3}{5}$,AH=$\frac{9}{5}$,
设AP=FP=x,则HP=$\frac{9}{5}$-x,
∵Rt△PFH中,HP2+HF2=PF2,即($\frac{9}{5}$-x)2+($\frac{3}{5}$)2=x2,
解得x=1,即AP=1.
综上所述,AP的长为1或$\frac{9}{4}$.
点评 本题考查了折叠问题,矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质以及勾股定理.解题时注意:折叠前后两图形全等,即对应线段相等;对应角相等.本题有两种情况,需要分类讨论,避免漏解.


科目:初中数学 来源: 题型:解答题
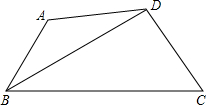 如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,
如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
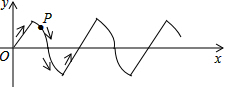 在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )| A. | ($\frac{2017}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{2017}{2}$,-$\frac{\sqrt{3}}{2}$) | C. | (2017,$\sqrt{3}$) | D. | (2017,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
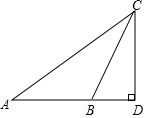 如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)
如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
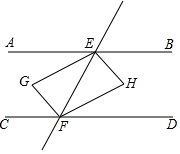 如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.
如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-3=$\frac{1}{2}$ | B. | x2=1 | C. | 2x+y=1 | D. | $\frac{2}{x}-1=0$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的顶点A(-1,0),B(3,0),D(-1,2),CD交y轴于E;抛物线y=ax2+bx+c经过点A,B,且该抛物线的顶点为M.
如图,矩形ABCD的顶点A(-1,0),B(3,0),D(-1,2),CD交y轴于E;抛物线y=ax2+bx+c经过点A,B,且该抛物线的顶点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com