
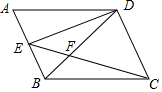
 如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:
如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行线性质求出∠ABC=∠ADC,得出平行四边形ABCD,即可推出AB∥CD;根据等腰三角形性质求出DE⊥AB,然后根据平行线的性质即可推出DE⊥CD;由∠A=∠ABD,四边形ABCD是平行四边形,可得AD=BD=BC,进而由等边对等角可得:∠BDC=∠BCD,然后由AD∥BC,可得∠ADB=∠DBC,然后由角的和差计算及等量代换可得:∠ADC-∠DCE=∠DBC+∠BCF,然后根据外角的性质可得:∠DFC=∠DBC+BCF,进而可得:∠DFC=∠ADC-∠DCE;根据等底等高的三角形面积相等即可推出S△EDF=S△BCF.
解答 解:∵AD∥BC,
∴∠A+∠ABC=180°,∠ADC+∠BCD=180°,
∵∠A=∠BCD,
∴∠ABC=∠ADC,
∵∠A=∠BCD,
∴四边形ABCD是平行四边形,
∴AB∥CD,
∵∠A=∠ABD,DE平分∠ADB,
∴DE⊥AB,
∴DE⊥CD,
∵∠A=∠ABD,四边形ABCD是平行四边形,
∴AD=BD=BC,
∴∠BDC=∠BCD,
∵AD∥BC,
∴∠ADB=∠DBC,
∵∠ADC=∠ADB+∠BDC,
∴∠ADC=∠DBC+∠BCD,
∴∠ADC-∠DCE=∠DBC+∠BCD-∠DCE=∠DBC+∠BCF,
∵∠DFC=∠DBC+∠BCF,
∴∠DFC=∠ADC-∠DCE,
∵∠CDF=∠ADC-∠ADB,∠DCE≠∠DBC,
∴∠CDF≠∠CFD.
∵AB∥CD,
∴△BED的边BE上的高和△EBC的边BE上的高相等,
∴由三角形面积公式得:S△BED=S△EBC,
都减去△EFB的面积得:S△EDF=S△BCF,
∴①②③正确,
故选C.
点评 本题考查了平行四边形的性质和判定,平行线性质,等腰三角形的性质,三角形的面积的应用,关键是推出AB∥CD.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16(1+a)2=25 | B. | 25(1-2a)=16 | C. | 25(1-a)2=16 | D. | 25(1-a2)=16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm,6cm,11cm | B. | 4cm,5cm,lcm | C. | 3cm,4 cm,5 cm | D. | 2cm,3 cm,6 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
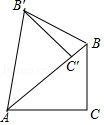 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠C′B′B的度数为( )| A. | 40° | B. | 50° | C. | 70° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.28×10-6米 | B. | 2.8×10-8米 | C. | 2.8×10-7米 | D. | 2.8×10-6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
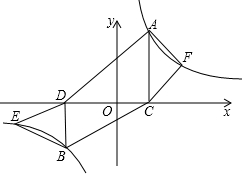 如图,点A和点F,点B和点E分别是反比例函数y=$\frac{4}{x}$图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为12-6$\sqrt{3}$.
如图,点A和点F,点B和点E分别是反比例函数y=$\frac{4}{x}$图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为12-6$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com