
【题目】如图已知数轴上点A、B分别表示a、b,且|b+6|与(a﹣9)2互为相反数,O为原点.
(1)a= ,b= ;
(2)若将数轴折叠点A与表示﹣10的点重合,则与点B重合的点所表示的数为 ;
(3)若点M、N分别从点A、B同时出发,点M以每秒1个单位长度的速度沿数轴向左匀速运动,点N以每秒2个单位长度的速度沿数轴向右匀速运动,N到点A后立刻原速返回,设运动时间为t(t>0)秒.①点M表示的数是 (用含t的代数式表示);②求t为何值时,2MO=MA;③求t为何值时,点M与N相距3个单位长度.
![]()
【答案】(1)a=9,b=﹣6;(2)与点B重合的点所表示的数为5;(3)①点M表示的数是9﹣t;②
t为4或6或12或18秒时,点M与N相距3个单位长度.
【解析】
(1)根据非负数的性质即可求解;
(2)先求出折叠点,依此可求与点B重合的点所表示的数;
(3)①根据路程=速度×时间可求点M表示的数;
②分M在原点右边和原点左边两种情况进行讨论可求t的值;
③分点M与N第一次相遇前后,点M与N第二次相遇前后,进行讨论可求t的值.
解:(1)依题意有|b+6|+(a﹣9)2=0,
b+6=0,a﹣9=0,
解得a=9,b=﹣6;
(2)(9﹣10)÷2=﹣0.5,
﹣0.5+6=5.5,
﹣0.5+5.5=5.
故与点B重合的点所表示的数为5;
(3)①点M表示的数是9﹣t;
②M在原点右边时,
依题意有2(9﹣t)=t,解得t=6;
M在原点左边边时,
依题意有﹣2(9﹣t)=t,解得t=18.
故t为6或18秒时,2MO=MA;
③点M与N第一次相遇前,
依题意有3t=15﹣3,
解得t=4;
点M与N第一次相遇后,
依题意有3t=15+3,
解得t=6;
(6+9)÷2=7.5(秒),
点M与N第二次相遇前,
2(t﹣7.5)﹣(t﹣7.5)=7.5﹣3,
解得t=12;
点M与N第二次相遇后,
2(t﹣7.5)﹣(t﹣7.5)=7.5+3,
解得t=18.
故t为4或6或12或18秒时,点M与N相距3个单位长度.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某的士的起步价为10元(可以坐3千米的路程),若超过3千米,则超出部分每千米另外加收2 元.
(1)小明坐该的士走了x千米的路程,应该付费多少元?
(2)小芳坐该的士走了18千米的路程,应该付费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
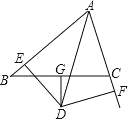
【题目】如图,G 为 BC 的中点,且 DG⊥BC,DE⊥AB 于 E,DF⊥AC 于 F, BE=CF.
(1)求证:AD 是∠BAC 的平分线;
(2)如果 AB=8,AC=6,求 AE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下统计图表:
频数分布表
身高分组/cm | 频数 | 百分比 |
| 5 | 10% |
| 20% | |
| 15 | 30% |
| 14 | |
| 6 | 12% |
总计 | 100% |
(1)填空:![]() ______;
______;
(2)通过计算补全频数分布直方图;
(3)该校九年级一共有600名学生,估计身高不低于165cm的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=![]() AB中,一定正确的是( )
AB中,一定正确的是( )
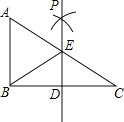
A.①②③ B.①②④ C.①③④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com