
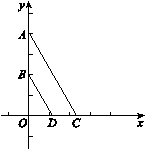
已知:如图,在平面直角坐标系xOy中,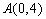 ,
,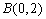 ,点C在x轴的正半轴上,
,点C在x轴的正半轴上,
点D为OC的中点.
(1) 求证:BD∥AC;
(2) 当BD与AC的距离等于1时,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
解:(1)
(2)

(3)
 |
解:(1)∵ 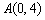 ,
,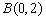 ,
,
∴ OA=4,OB=2,点B为线段OA的中点.
∵ 点D为OC的中点,
∴ BD∥AC.
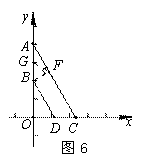
(2)如图6,作BF⊥AC于点F,取AB的中点G,则 .
.
∵ BD∥AC,BD与AC的距离等于1,
∴  .
.
∵ 在Rt△ABF中, ,AB=2,点G为AB的中点,
,AB=2,点G为AB的中点,
∴ 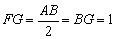 .
.
∴ △BFG是等边三角形, .
.
∴ 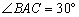 .
.
设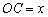 ,则
,则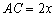 ,
,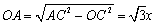 .
.
 |
∵ OA=4,
∴ 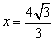 .
.
∵ 点C在x轴的正半轴上,
∴ 点C的坐标为 .
.
(3)如图7,当四边形ABDE为平行四边形时,AB∥DE.
∴ DE⊥OC.
∵ 点D为OC的中点,
∴ OE=EC.
∵ OE⊥AC,
∴ 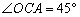 .
.
∴ OC=OA=4.
∵ 点C在x轴的正半轴上,
∴ 点C的坐标为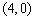 .
.
设直线AC的解析式为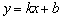 (k≠0).
(k≠0).
则 解得
解得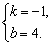
∴ 直线AC的解析式为 .
.



 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
已知:如图,点A是直线l外一点,B,C两点在直线l上,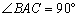 ,
, .
.
(1)按要求作图:(保留作图痕迹)
①以A为圆心,BC为半径作弧,再以C为圆心,AB为半径作弧,两弧交于点D;
②作出所有以A,B,C,D为顶点的四边形;
(2)比较在(1)中所作出的线段BD与AC的大小关系.
解:(1)

(2)BD AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
有五张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是
A.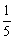 B.
B.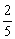 C.
C.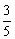 D.
D.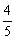
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com