
| |||||||||||
(1) |
如图,连结OP.
因为弦PD⊥直径BE于C,所以∠D+∠AOD= |
(2) |
因为OC∶CB=l∶2,所以设OC=x,则BC=2x,所以OB=3x=OP, 在Rt△ACP与Rt△APO中,因为∠ACP=∠APO= 所以△ACP∽△APO,所以 因为∠APO= 所以sinA= |


科目:初中数学 来源: 题型:
 12、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C
12、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C查看答案和解析>>
科目:初中数学 来源:2012-2013学年吉林省镇赉县保民中学七年级下第一次月考数学试卷(带解析) 题型:解答题
如图所示,BE是∠ABC的平分线,∠1=∠2,试说明DE∥BC.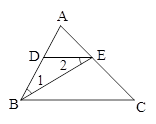
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com