
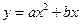 (a
(a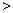 0)与双曲线
0)与双曲线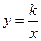 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).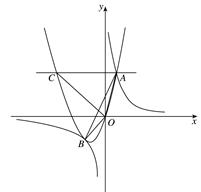
(第12题) |
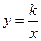 上,
上,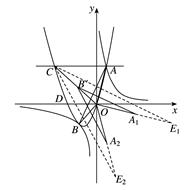 所以k=4. 故双曲线的函数表达式为
所以k=4. 故双曲线的函数表达式为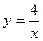 .
.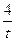 ),
),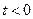 ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为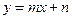 ,则有
,则有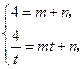 解得
解得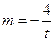 ,
, .
.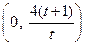 ,故
,故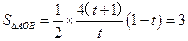 ,整理得
,整理得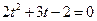 ,
,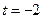 ,或t=
,或t=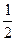 (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为(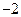 ,
,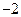 ).
).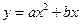 (a
(a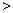 0)上,所以
0)上,所以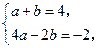 得
得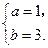 …………(10分)
…………(10分)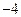 ,4),于是CO=4
,4),于是CO=4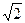 . 又BO=2
. 又BO=2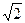 ,所以
,所以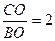 .
.
|
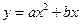 (a
(a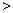 0)与x轴负半轴相交于点D, 则点D的坐标为(
0)与x轴负半轴相交于点D, 则点D的坐标为(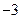 ,0).因为∠COD=∠BOD=
,0).因为∠COD=∠BOD=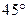 ,所以∠COB=
,所以∠COB=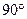 .
.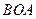 绕点O顺时针旋转
绕点O顺时针旋转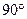 ,得到△
,得到△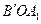 .这时,点
.这时,点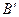 (
(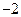 ,2)是CO的中点,点
,2)是CO的中点,点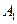 的坐标为(4,
的坐标为(4,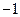 ).
).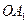 到点
到点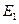 ,使得
,使得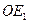 =
=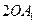 ,这时点
,这时点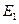 (8,
(8,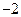 )是符合条件的点.
)是符合条件的点.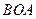 关于x轴的对称图形△
关于x轴的对称图形△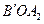 ,得到点
,得到点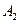 (1,
(1,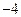 );延长
);延长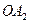 到点
到点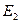 ,使得
,使得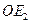 =
=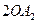 ,这时点E2(2,
,这时点E2(2,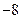 )是符合条件的点.
)是符合条件的点.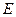 的坐标是(8,
的坐标是(8,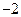 ),或(2,
),或(2, ). …………(20分)解析:
). …………(20分)解析:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
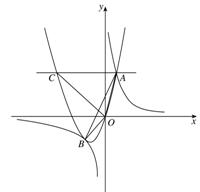
如图,抛物线![]() (a
(a![]() 0)与反比例函数
0)与反比例函数![]() 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
1.求反比例函数的解析式
2.用含t的代数式表示直线AB的解析式;
3.求抛物线的解析式;
4.过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
查看答案和解析>>
科目:初中数学 来源:2011年安徽省中考压轴题预测试数学卷 题型:解答题
如图,抛物线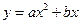 (a
(a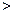 0)与反比例函数
0)与反比例函数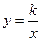 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)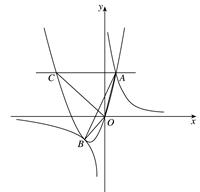
【小题1】求反比例函数的解析式
【小题2】用含t的代数式表示直线AB的解析式;
【小题3】求抛物线的解析式;
【小题4】过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省九年级下学期第一次模拟数学卷(解析版) 题型:解答题
如图,抛物线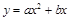 (a
(a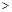 0)与双曲线
0)与双曲线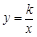 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
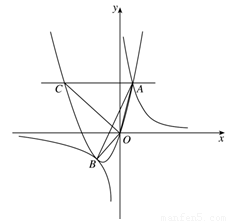
(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标. (其中点E和点A,点C和点B分别是对应点)
查看答案和解析>>
科目:初中数学 来源:2011年安徽省考压轴题预测试数学卷 题型:选择题
如图,抛物线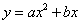 (a
(a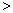 0)与反比例函数
0)与反比例函数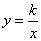 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
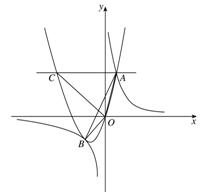
1.求反比例函数的解析式
2.用含t的代数式表示直线AB的解析式;
3.求抛物线的解析式;
4.过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com