
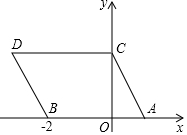
 如图,在平面直角坐标系中,点A、B的坐标分别为(1,0)、(-2,0),现同时将点A、B分别向上平移2个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、CD.
如图,在平面直角坐标系中,点A、B的坐标分别为(1,0)、(-2,0),现同时将点A、B分别向上平移2个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、CD.分析 (1)根据题意得C(0,2),于是得到结论;
(2)根据已知条件得到OB=2,求得OC=2,CD=3,点P在线段BD上运动,当点P运动到端点B时,△PCO的面积最小,为$\frac{1}{2}$•BO•CO=$\frac{1}{2}×$2×2=2,当点P运动到端点D时,△PCO的面积最大,为$\frac{1}{2}$•CD•OC=$\frac{1}{2}$×3×2=3,于是得到结论;
(3)分三种情况,根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE即可得出结论.
解答 解:(1)由题意,得C(0,2),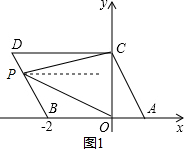
∴□ABDC的高为2,
若S△ABM=S□ABDC,则△ABM的高为4,
又∵点M是y轴上一点,
∴点M的坐标为(0,4)或(0,-4);
(2)∵B(-2,0),O(0,0),
∴OB=2,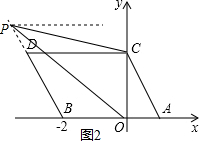
由题意,得C(0,2),D(-3,2),
∴OC=2,CD=3,
∴S梯形OBDC=$\frac{OB+CD}{2}$×OC=$\frac{2+3}{2}$×2=5,
∵点P在线段BD上运动,
当点P运动到端点B时,△PCO的面积最小,为$\frac{1}{2}$•BO•CO=$\frac{1}{2}×$2×2=2,
当点P运动到端点D时,△PCO的面积最大,为$\frac{1}{2}$•CD•OC=$\frac{1}{2}$×3×2=3,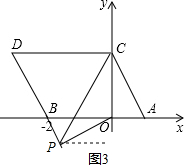
∴S=S△PCD+S△POB=S梯形OBDC-S△PCO=5-S△PCO,
∴S的最大值为5-2=3,最小值为5-3=2,
故S的取值范围是:2≤S≤3;
(3)如图:
当点P在线段BD上运动时,∠CPO=∠DCP+∠BOP;
当点P在射线BD上运动时,∠CPO=∠BOP-∠DCP;
当点P在射线DB上运动时,∠CPO=∠DCP-∠BOP.
点评 此题是四边形综合题,主要考查了平移的平移的性质,平行线的性质,三角形的面积公式,平行四边形的面积计算方法,解本题的关键是作出图形,是一道比较简单的中考常考题.


科目:初中数学 来源: 题型:选择题
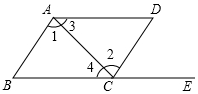 如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )
如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠B=∠DCE | D. | ∠D+∠DAB=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
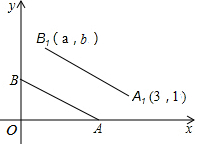 如图所示,A、B的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB.若A1、B1的坐标分别为(3,1),(a,b),则a+b的值为( )
如图所示,A、B的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB.若A1、B1的坐标分别为(3,1),(a,b),则a+b的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com