
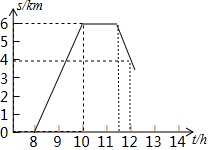
 某班师生组织植树活动,上午8时从学校出发,到达植树地点后植树1.5h,然后按原路返回,如图为师生离校路程s(km)与时间t(h)之间的函数关系图象,则师生回到学校的时间为( )
某班师生组织植树活动,上午8时从学校出发,到达植树地点后植树1.5h,然后按原路返回,如图为师生离校路程s(km)与时间t(h)之间的函数关系图象,则师生回到学校的时间为( )| A. | 12时30分 | B. | 12时45分 | C. | 13时 | D. | 13时30分 |
分析 设直线解析式为s=kt+b,然后利用待定系数法确定其解析式得s=-4t+52,再令s=0时,求出t的值,即可得到师生回到学校的时间.
解答 解:如图,设直线AB的解析式为s=kt+b,
把(11.5,6),(12,4)分别代入得
$\left\{\begin{array}{l}{6=11.5k+b}\\{4=12k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-4}\\{b=52}\end{array}\right.$,
∴直线AB的解析式为s=-4t+52,
令s=0,则-4t+52=0,
解得t=13,
则师生13时回到学校;
故选C.
点评 本题考查了一次函数的应用:先把实际问题中的数据与坐标系中的数据对应起来,利用待定系数法确定一次函数的解析式,然后利用一次函数的性质解决问题.


科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3,6 | B. | 6,-3 | C. | 1,2 | D. | 0,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
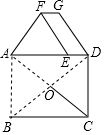 如图,在矩形ABCD中,AB=6,BC=8,AC和BD相交于点O,将△ABO绕点A逆时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到线段DG,则FG的长为( )
如图,在矩形ABCD中,AB=6,BC=8,AC和BD相交于点O,将△ABO绕点A逆时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到线段DG,则FG的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
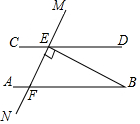 如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )
如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )| A. | 55° | B. | 35° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
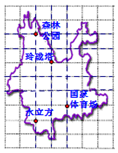 “健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一艘船由A港沿北偏西60°方向航行10海里至B港,然后再沿北偏东30°方向航行10海里至C港.则下列说法正确的是( )
如图,一艘船由A港沿北偏西60°方向航行10海里至B港,然后再沿北偏东30°方向航行10海里至C港.则下列说法正确的是( )| A. | C港在A港的南偏西30°方向上 | B. | C港在A港的北偏西30°方向上 | ||
| C. | C港在A港的北偏西15°方向上 | D. | C港在A港的南偏西15°方向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com