
【题目】已知在![]() 中,∠C=90°,AC=8,BC=6,
中,∠C=90°,AC=8,BC=6,
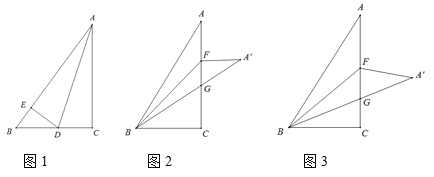
(1)若AD是∠BAC的角平分线,AD交BC边于D,过点D作DE⊥AB与点E(如图1),请求出BE的长及![]() 的值;
的值;
(2)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若BC=CF,如图2,请证明
与AC交于点G,若BC=CF,如图2,请证明![]() ∽
∽![]() ;
;
(3)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若
与AC交于点G,若![]() ,如图3,请求出
,如图3,请求出![]() 的值(可以直接利用第(1)题求出的结论)
的值(可以直接利用第(1)题求出的结论)
【答案】(1)![]() ;
; ![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)设CD=DE=x,则BD=6-x,通过![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,证明△ADE≌△ADC(AAS),可得CD=DE,AE=AC=8,推出
,证明△ADE≌△ADC(AAS),可得CD=DE,AE=AC=8,推出![]() ,再根据勾股定理构建方程即可解决问题.
,再根据勾股定理构建方程即可解决问题.
(2)设![]() 的度数为
的度数为![]() ,由折叠可得
,由折叠可得![]() ,根据
,根据![]() ,
,![]() ,
,
可得![]() ,利用折叠和三角形的外角的性质,可得
,利用折叠和三角形的外角的性质,可得![]() ,则可证
,则可证![]() ∽
∽![]()
(3)作A′H⊥AC于H,设![]() 的长度为
的长度为![]() ,利用
,利用![]() ≌
≌![]() ,
,![]() ∥
∥![]() ,得到
,得到![]() ,由(1)得
,由(1)得![]() ,则
,则![]() ,解得
,解得![]() ,则有
,则有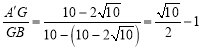 .
.
解:∵∠C=90°,AC=8,BC=6,
∴AB=10,
(1)设![]() 的长度为
的长度为![]() ,则
,则![]()
∵![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]()
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (AAS)
(AAS)
∴![]()
∴![]()
在直角![]() 中,
中,![]()
∴![]()
解得![]()
∴![]()
综上所述,![]() ,
,![]()
(2)设![]() 的度数为
的度数为![]() ,由折叠可得
,由折叠可得![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]() ∽
∽![]()
(3)如图,过点![]() 作
作![]() 交
交![]() 于
于![]() 点,
点,
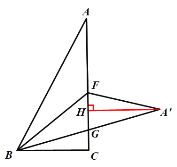
设![]() 的长度为
的长度为![]() ,由折叠可得
,由折叠可得![]() ≌
≌![]()
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]() ∥
∥![]()
∴![]()
由(1)得![]()
∴![]()
∴![]()
解得![]()
∴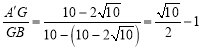


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
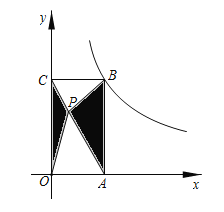
【题目】如图,在平面直角坐标系中,矩形OABC顶点A、C分别在x轴、y轴的正半轴上,顶点B在反比例函数y=![]() (x>0)的图象上,点P是矩形OABC内的一点,连接PO、PA、PB、PC,若图中阴影部分的面积10,则k为__.
(x>0)的图象上,点P是矩形OABC内的一点,连接PO、PA、PB、PC,若图中阴影部分的面积10,则k为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
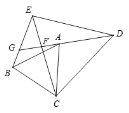
【题目】如图,已知△ABC和△DCE是等边三角形,连接BE,连接DA并延长交CE于点F,交BE于点G,CD=6,EF=2,那么EG的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
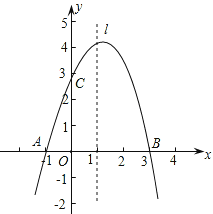
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,AD=8,O为AD中点,P是线段AO上一动点,以O为圆心,OP为半径作⊙O分别交BO及BO延长线于点E,F,延长AE交BC于点H.
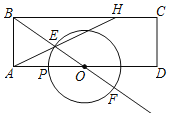
(1)当OP=2时,求BH的长.
(2)当AH交⊙O于另一点G时,连接FG,DF,作DM⊥BF于点M,求证:△EFG∽△FDM.
(3)连结HO,当△EHO是直角三角形时,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
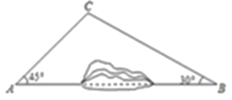
【题目】为加快城乡对接,建设美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山.汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=100千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地要走多少千米?
(2)开通隧道后,汽车从A地到B地可以少走多少千米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com