
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上的动点,且DE=CF,连接DF、AE,AE的延长线交DF于点M,连接OM.
(1)求证:△ADE≌△DCF;
(2)求证:AM⊥DF;
(3)当CD=AF时,试判断△MOF的形状,并说明理由.

【答案】(1)证明见解析;(2)证明见解析.(3)△MOF是等腰三角形,理由见解析.
【解析】
(1)根据DE=CF和正方形的性质,证明△AED≌△DFC;
(2)由△AED≌△DFC得出∠EAD=∠FDC,然后利用等角代换可得出∠AMD=90°,得出了结论.
(2)利用等腰三角形三线合一得:DM=FM,再由直角三角形斜边中线可得结论.
(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠DCF=45°
在△AED和△DFC中,
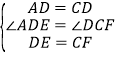 ,
,
∴△AED≌△DFC(SAS);
(2)由①中△AED≌△DFC,
∴∠EAD=∠FDC,
∵∠ADM+∠FDC=90°,
∴∠ADM+∠EAD=90°,
∴∠AMD=90°,
∴AM⊥DF;
(3)△MOF是等腰三角形,
理由是:∵AD=CD,CD=AF
∴AD=AF
∵AM⊥DF,
∴DM=FM,
∵∠DOF=90°,
∴OM=![]() DF=FM,
DF=FM,
∴△MOF是等腰三角形.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,绘出了某一结果出现的频率的折线图,则符合这一结果的实验可能是
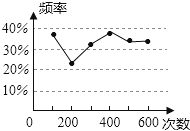
A. 掷一枚正六面体的骰子,出现1点的概率
B. 抛一枚硬币,出现正面的概率
C. 任意写一个整数,它能被2整除的概率
D. 从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
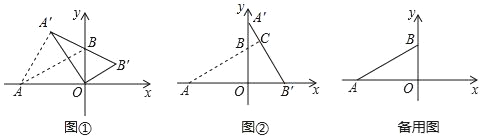
(1)如图①,当点A′,B,B′共线时,求AA′的长.
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,∠AOB=60°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
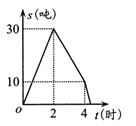
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 过点
过点![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,作
,作![]() 轴于点
轴于点![]() .设点
.设点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() .
.

(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)探究:是否存在这样的点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)设![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )

A. 10B. 4![]() C. 20D. 8
C. 20D. 8![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com