
【题目】某班数学兴趣小组对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数, ![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
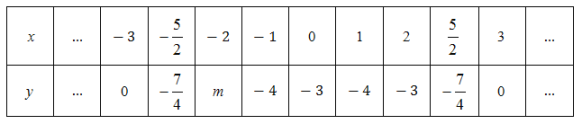
其中,![]() ________.
________.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
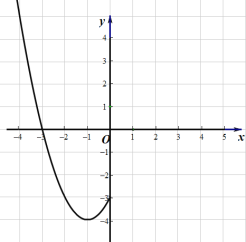
(3)观察函数![]() 图象,回答下列问题:
图象,回答下列问题:
①函数图像的对称性是: .
②当![]() 时,写出
时,写出![]() 随
随![]() 的变化规律: .
的变化规律: .
(4)进一步探究函数图象发现:方程![]() 有________个实数根.
有________个实数根.
【答案】(1)-3;(2)见解析;(3)①关于![]() 轴对称;②当
轴对称;②当![]() 时
时![]() 随
随![]() 的增大而减小,当
的增大而减小,当![]() 时
时![]() 随
随![]() 的增大而增大;(4)3.
的增大而增大;(4)3.
【解析】
(1)根据已知,将![]() 及其对应的自变量
及其对应的自变量![]() 代入函数解析式,即可求得
代入函数解析式,即可求得![]() 的值;
的值;
(2)根据表格中的数据,进行描点即可画出函数图象;
(3)观察函数图象即可得出对称性和![]() 时,
时,![]() 随
随![]() 的变化规律,分为
的变化规律,分为![]() 时和
时和![]() 时两种情况;
时两种情况;
(4)直接观察图象即可得解.
(1)由已知,将![]() 及其对应的自变量
及其对应的自变量![]() 代入函数解析式,得
代入函数解析式,得
![]()
![]()
(2)如图所示:

(3)观察函数![]() 图象,回答下列问题:
图象,回答下列问题:
①函数图像的对称性是: 关于![]() 轴对称
轴对称
②当x > 0时,写出y随x的变化规律: 当![]() 时
时![]() 随
随![]() 时
时![]() 随
随![]() 的增大而增大 ;
的增大而增大 ;
(4)进一步探究函数图象发现:方程![]() 有__
有__![]() __个实数根.
__个实数根.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中点,到点O的距离等于![]() BC的所有点组成的图形记为G,图形G与AB交于点D.
BC的所有点组成的图形记为G,图形G与AB交于点D.

(1)补全图形并求线段AD的长;
(2)点E是线段AC上的一点,当点E在什么位置时,直线ED与 图形G有且只有一个交点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
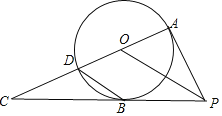
【题目】如图,PA是⊙O的切线,A为切点.B为⊙O上一点,连接AO并延长,交⊙O于点D.交PB的延长线于点C连接PO,若PA=PB.
(1)求证:PB是⊙O的切线;
(2)连接DB,若∠C=30°,求证:D是CO的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
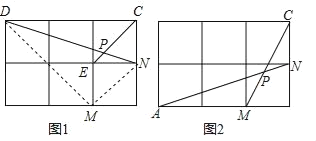
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=x2+bx+c经过点A(2,﹣3)与C(0,﹣3),与x轴负半轴的交点为B.
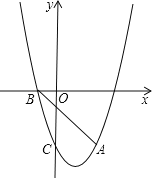
(1)求抛物线的解析式与点B坐标;
(2)若点D在x轴上,使△ABD是等腰三角形,求所有满足条件的点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,若以A、B、M、N为顶点的四边形是平行四边形,其中AB∥MN,请直接写出所有满足条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
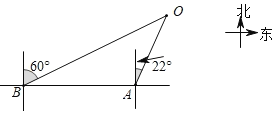
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
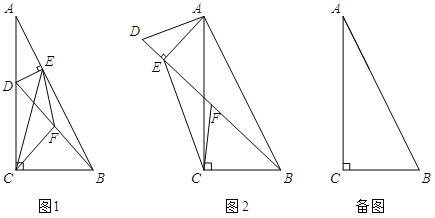
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com