
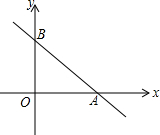
 如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B,点M在x轴上,要使△ABM是以AB为腰的等腰三角形,那么点M的坐标是($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0).
如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B,点M在x轴上,要使△ABM是以AB为腰的等腰三角形,那么点M的坐标是($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0). 分析 分别令一次函数y=-x+1中x=0、y=0,求出点A、B的坐标,设出点M的坐标,根据两点间的距离公式表示出AB、AM和BM的长度,分AB=BM与AB=AM两种情况来考虑,由此可得出关于m的方程,解关于m的方程即可得出结论.
解答 解:令一次函数y=-x+1中y=0,则-x+1=0,
解得:x=1,
∴点A的坐标为(1,0);
令一次函数y=-x+1中x=0,则y=1,
∴点B的坐标为(0,1).
设点M的坐标为(m,0),则AB=$\sqrt{2}$,AM=|m-1|,BM=$\sqrt{(0-m)^{2}+(1-0)^{2}}$,
△ABM是以AB为腰的等腰三角形分两种情况:
①AB=AM,即$\sqrt{2}$=|m-1|,
解得:m=$\sqrt{2}$+1,或m=-$\sqrt{2}$+1,
此时点M的坐标为($\sqrt{2}$+1,0)或(-$\sqrt{2}$+1,0);
②AB=BM,即$\sqrt{2}$=$\sqrt{(0-m)^{2}+(1-0)^{2}}$,
解得:m=-1,或m=1(舍去),
此时点M的坐标为(-1,0).
综上可知点M的坐标为($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0).
点评 本题考查了一次函数图象上点的坐标特征以及等腰三角形的性质,解题的关键是分AB=BM与AB=AM两种情况来考虑.本题属于基础题,难度不大,解决该题型题目时,有两点间的距离公式表示出三角形三边长度,再根据等腰三角形的性质找出关于m的方程是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
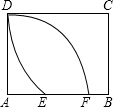 如图所示,以矩形的顶点A为圆心AD的长为半径画圆交AB于点F,再以C为圆心CD的长为半径画圆,交AB于点E,若AD=5,CD=$\frac{17}{3}$,则EF的长是2.
如图所示,以矩形的顶点A为圆心AD的长为半径画圆交AB于点F,再以C为圆心CD的长为半径画圆,交AB于点E,若AD=5,CD=$\frac{17}{3}$,则EF的长是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
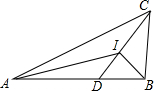 如图,在△ABC中,AB=6,BC=3,CA=7,I为△ABC的内心,连接CI并延长交AB于点D.记△CAI的面积为m,△DAI的面积为n,则$\frac{m}{n}$=( )
如图,在△ABC中,AB=6,BC=3,CA=7,I为△ABC的内心,连接CI并延长交AB于点D.记△CAI的面积为m,△DAI的面积为n,则$\frac{m}{n}$=( )| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
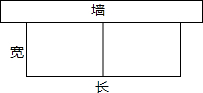 有长为30m的篱笆,一面利用墙(墙的可用长度不能超过16m)围成一块矩形花圃,如图所示:
有长为30m的篱笆,一面利用墙(墙的可用长度不能超过16m)围成一块矩形花圃,如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥-1 | B. | a≤1 | C. | 0<a≤1 | D. | -1≤a≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com